مُنحنی‌های ریاضی- Mathematical curves

خَم یا منحنی یک مفهوم هندسی است. در ریاضیات، مفهوم منحنی (خم) برای نشان دادن یک شیء یک بعدی و پیوسته به کار می‌رود. یک مثال ساده دایره‌ است. در گفتگوی روزمره یک خط صاف، منحنی در نظر گرفته نمی‌شود ولی در مکالمه‌ی ریاضیاتی خط‌های مستقیم و پاره خط‌ها نیز خم‌اند. در هندسه منحنی‌های بسیاردیگری مطالعه می‌شوند. هم‌چنین، منحنی(خم) می‌تواند هم معنی با تابع ریاضی یا نمودار تابع باشد.

بطور کلی، خم یا منحنی به دو گونه‌است:

• منحنی مسطح: خمی است که بر روی سطح دوبعدی (صفحه) قابل جایگیری است.
• منحنی کج: خمی فضایی است که روی هیچ صفحه‌ای قرار نگیرد.

منحنی مسطح

بطور شهودی، خم مسطح به مجموعه‌ای از نقطه‌ها گفته می‌شود، به شرط آن‌که بتوانیم بدون بلند کردن قلم از روی کاغذ آن را رسم کنیم. منحنی‌های مسطح به سه نوع زیر تقسیم می‌شوند:

• منحنی ساده: یک منحنی ساده، یک منحنی مسطح است که هیچ یک از نقطه های خود را قطع نکند.
• منحنی بسته: به خمی اطلاق می‌شود که نقطه‌های (انتهایی) آن به هم رسیده (و بر یکدیگر منطبق) باشند.
• منحنی ساده بسته: منحنی ای ساده بسته است که نقطه‌های ابتدا و انتهایی آن برهم منطبق باشند و نقطه‌های خود را قطع نکند.

قضیه منحنی جُردن: هر منحنی سادهٔ بسته C، صفحه را به سه زیر مجموعهٔ جدا از هم درون، بیرون و روی منحنی تقسیم می‌کند.

درتوپولوژی، منحنی را به صورت زیر تعریف می کنیم:

فرض کنیم I بازه‌ای‌ست از اعداد حقیقی (یعنی یک زیر مجموعه همبند ناتهی از). آنگاه، خم یک نگاشت پیوسته  است که X یک فضای توپولوژیکی است.

خم  را ساده می‌گویند اگر که برای هر x،y در I داشته باشیم:

در صورتی که، I بازه‌ای بسته و کراندار باشد، امکان را هم مجاز در نظر می گیریم (این قرارداد امکان این را می‌دهد که راجع به خم سادهٔ بسته صحبت کنیم).

چنانچه، به ازاء برخی  (غیر از دوسر I) داشته باشیم:

آنگاه به  یک نقطهٔ مضاعف (یا چندگانه)از خم گفته می‌شود.

خم  را بسته یا یک حلقه می‌گوییم اگر و اگر . بنابراین یک خم بسته یک نگاشت پیوسته از دایره  است. یک خم ساده بسته همچنین یک خم ژوردان گفته می‌شود. یک خم صفحه‌ای خم‌ای است که برای آن X یک فضای اقلیدسی است—اینها مثال‌هایی هستند که ابتدا بیان شدند. یک خم فضایی خم‌ای است که برای آن X سه بعدی یا فضای اقلیدسی است. یک خم کج خم فضایی است که روی هیچ صفحه‌ای قرار نگیرد. این تعاریف همچنین در مورد خم‌های جبری نیز صادقند. اما در مورد خم جبر معمول است که خم را به داشتن نقاط تعریف شده روی اعداد حقیقی محدود نکنیم.

تفاوت بین یک منحنی و تصویرآن مهم است. دو منحنی متمایز ممکن است تصویر یکسان داشته باشند. به عنوان مثال یک پاره خط می‌تواند در سرعت‌های متفاوت پیموده شود، یا یک دایره می‌تواند به دفعات متفاوت پیموده شود. با این وجود خیلی اوقات ما فقط به تصویر منحنی علاقه‌مندیم. مهم است که هنگام مطالعه به زمینه و قرارداد توجه شود. اغلب توپولوژیست‌ها از اصطلاح «مسیر» به عنوان آنچه ما منحنی می‌نامیم و از «منحنی» به عنوان به عنوان آنچه ما تصویر می‌نامیم استفاده می‌کنند. درهندسه دیفرانسیل معمولا از اصطلاح «خم» استفاده می‌شود.

تصویر یک تابع: اگر f یک نگاشت، تابع یا تبدیل از دامنهٔ D به هم دامنه‌یY باشد. آنگاه تصویر f که گاه به آن برد f نیز گفته می‌شود مجموعهٔ مقادیری است که f با تغییر ورودی‌اش روی مقادیر D به دست می‌دهد. اصطلاح تصویر تابع در متون آکادمیک نسبت به برد ارجحیت دارد. تصویر تابع می‌تواند برای زیرمجموعه‌هایی از دامنه نیز تعریف شود. [f[a,b بیانگر تصویر بازه‌‌‌‌‌‌‌‌‌ ی [a,b] تحت تابع f است.

تصویر یک تابع زیر مجموعه‌ای از هم دامنه‌ی آن است.

در ابتدا سهمی ها را معرفی می‌کنیم. در متون علمی آمده است که:

• منایخموس ریاضیدان یونانی باستان سهمی را جهت حل مسئله تضعیف مکعب (ساختن مکعبی که حجم آن دو برابر حجم یک مکعب مفروض است فقط با استفاده از خطکش و پرگار)، مورد مطالعه قرار داد.
• اسحاق نیوتن در کتاب «اصول ریاضی فلسفه طبیعی» نشان داد که اگر نیروی کشش میان اجسام آسمانی متناسب با معکوس مجذور فاصله بین آن دو باشد، اجرامی که به دور یک جرم بزرگ می‌گرداند، یا باید حرکت دایره‌ای، بیضوی، سهموی یا هذلولوی داشته باشند. نیوتن از سهمی برای محاسبه مدار شهاب سنگ‌ها استفاده کرد. امروزه می‌دانیم که اگر چه سهمی مدل خوبی برای حرکت شهاب سنگ‌ها می‌باشد ولی این مدل از دقت بالایی برخوردار نیست و به ندرت مدار شهاب سنگ‌ها با دقت بسیار بالایی سهموی می‌باشند.
• گالیله نشان داد که وقتی جسمی را در هوا پرتاب می‌کنیم، مسیر حرکت آن سهموی می‌باشد. این موضوع زمانی صحت دارد که از مقاومت هوا و آثار چرخشی چشم پوشی شود.
• نیوتن و گرگوری نشان دادند که هنگامی که نور به صورت موازی به یک آینه سهموی تابانده شود، پس از انعکاس در کانون آن جمع می‌شود.
• پاسکال سهمی را تصویر یک دایره در نظر گرفت.
• اقتصادی‌ترین شکل پل کمانی در اغلب شرایط عملی سهمی می‌باشد.

منحنی سهمی – Partial curve

زمانی که شما به یک توپ فوتبال ضربه می‌زنید (یا تیری را از کمان رها کرده یا سنگی را به سمت آسمان پرتاب می‌کنید) پرتابه با طی کردن یک کمان به سمت بالا رفته و سپس سقوط می‌کند. مسیر پیموده‌شده توسط پرتابه بخشی از یک منحنی سهمی می‌باشد.

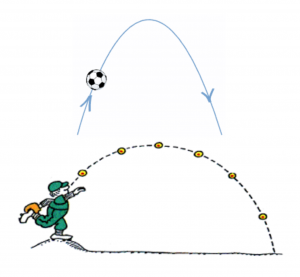
اجزای منحنی سهمی عبارت است از:

• خط هادی و کانون (در بالا شرح داده‌شده‌است.)
• محور تقارن (با عبور از کانون، بر خط هادی عمود می‌گردد.)
• رأس (نقطه‌ای که سهمی بیشترین پیچش خود را دارد و دقیقا میان کانون و خط هادی قرار دارد.)
  

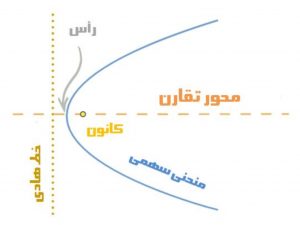
در ریاضیات سَهمی مکان هندسی نقاطی از صفحه است که از یک خط و از یک نقطه هم فاصله هستند. این منحنی که شَلجَمی هم نامیده می‌شود یکی ازمقاطع مخروطی می‌باشد، زیرا از تقاطع یک صفحه و یک مخروط می‌تواند بوجود بیاید.

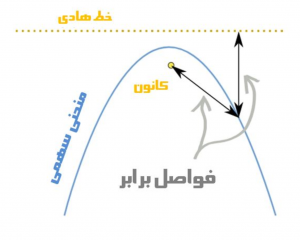
یکی از ویژگی های سهمی این است که هر پرتویی موازی با محور تقارن سهمی به آن تابیده شود پس از بازتاب از کانون عبور می‌کند. دلیل نامگذاری این نقطه نیز به خاطر همین ویژگی است. زیرا تمامی پرتو‌ها در این نقطه متمرکز می‌شوند.

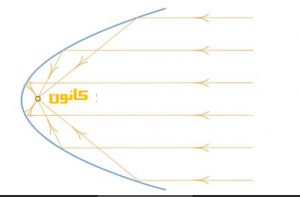
چند مورد از کاربرد منحنی های سهمی :

• دیش‌های ماهواره
• دیش‌های رادار
• متمرکزسازی تشعشعات خورشیدی جهت ایجاد یک نقطه‌ با دمای بالا
• ایجاد سطح بازتاب‌کننده روی نور افکن‌ها و چراغ‌قوه‌ها

همچنین با برش یک مخروط به‌وسیله یک صفحه (صفحه باید با سطح مخروط موازی باشد.) نیز می‌توان به یک سهمی دست‌پیدا‌نمود. بنابراین منحنی بدست‌آمده مقطعی از یک مخروط است.

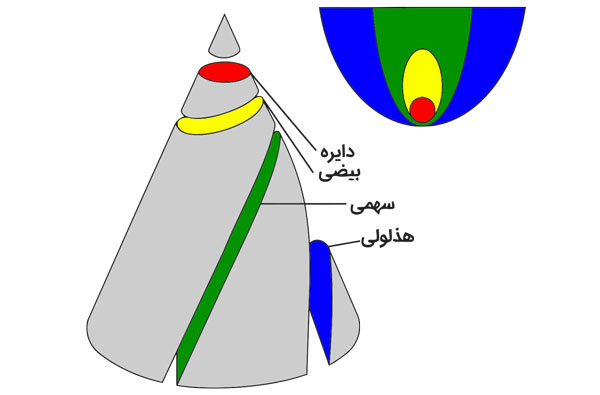
طول قوس منحنی

تاکنون از انتگرال معین عمدتاً برای محاسبه مساحت زیر نمودار استفاده کرده‌ایم. ولی انتگرال معین برای محاسبه طول قوس توابع نیز کاربرد دارد. یعنی به جای محاسبه مساحت زیر منحنی تابع، طول قوس خود منحنی را حساب کنیم. جهت محاسبه طول قوس منحنی (y=f(x در بازه [a,b] از رابطه زیر استفاده می‌کنیم:

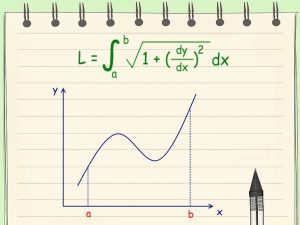
مثال: محیط دایره‌ای به شعاع  ۳ را به کمک انتگرال معین محاسبه کنید.

حل: معادله دایره به شعاع  ۳ عبارت است از

که برای نیم دایره بالایی داریم:

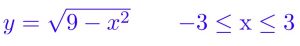
که مشتق آن برابر است با:

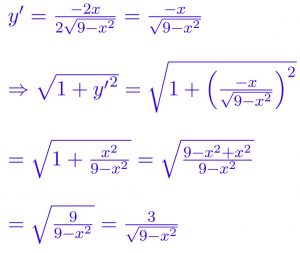
محیط دایره برابر است با ۲ برابر طول قوس نیم‌دایره بالایی:

رویه چیست؟ (?What is a surface)

در ریاضیات و به‌خصوص توپولوژی، رویه یا سطح یک منیفلد توپولوژیکی دوبعدی است. سطوح اجسام سه‌ بعدی مانند یک توپ مثال‌هایی ساده از این اشیاء ریاضی در فضای اقلیدسی ۳بعدی هستند. سطح‌هایی نیز مانند بطری کلاین وجود دارند که نمی‌توان آن‌ها را بدون ایجاد تکینگی یا قطع نمودن خود، در فضای سه‌بعدی اقلیدسی تصویر کرد.

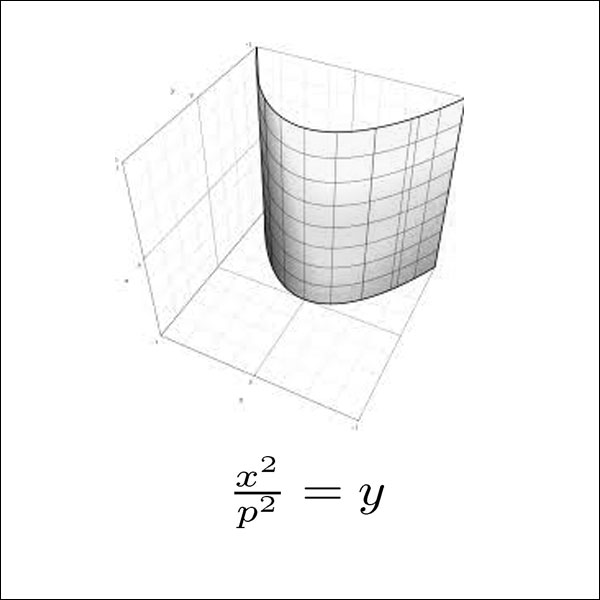
سطوح چهارگوش – Quadric surfaces

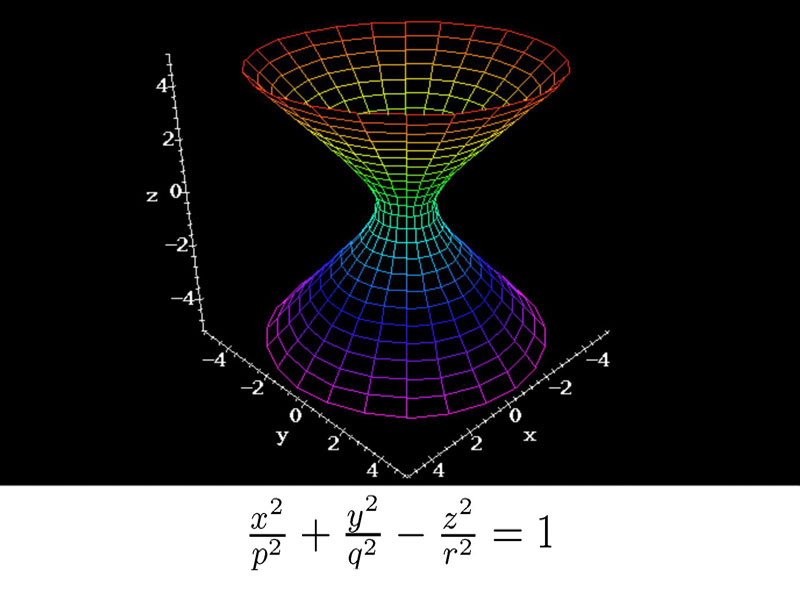
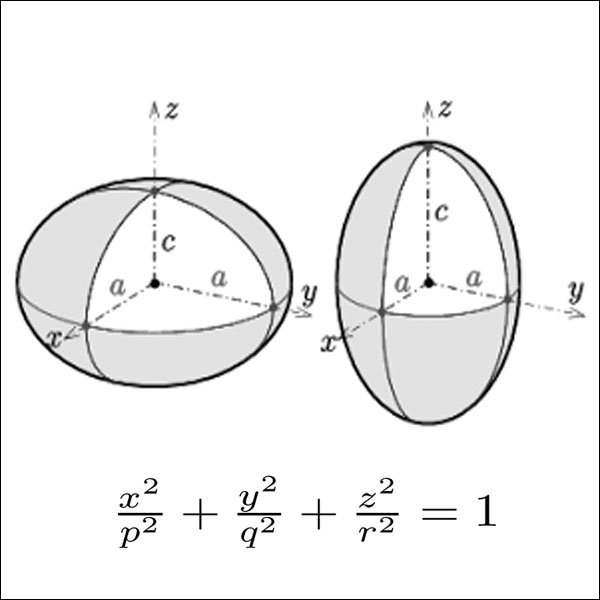
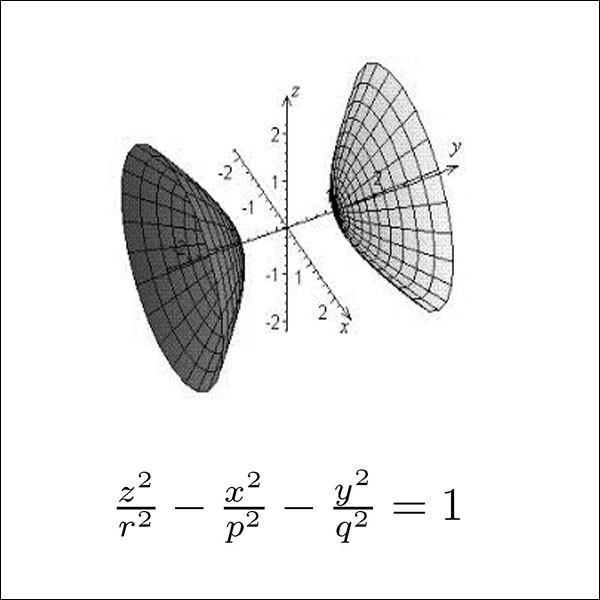
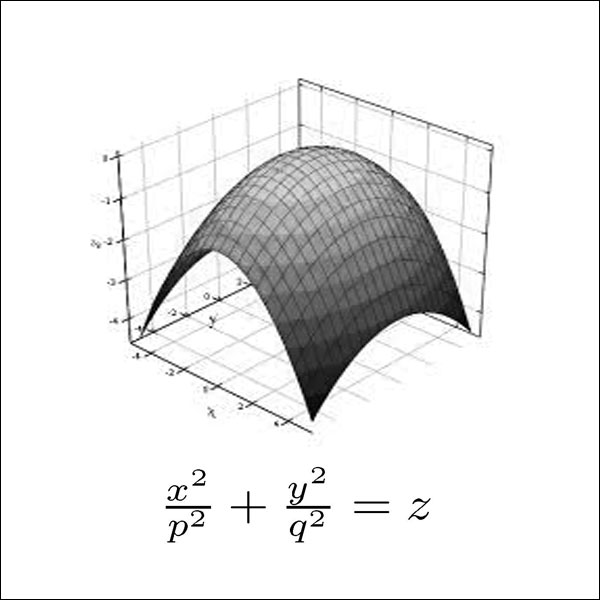
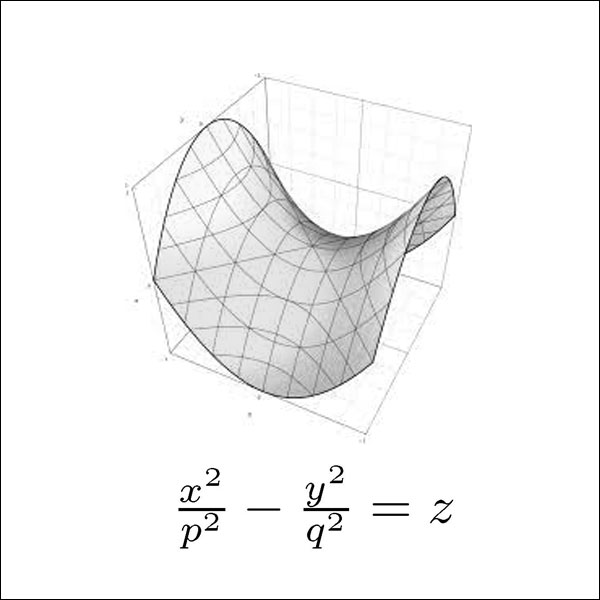
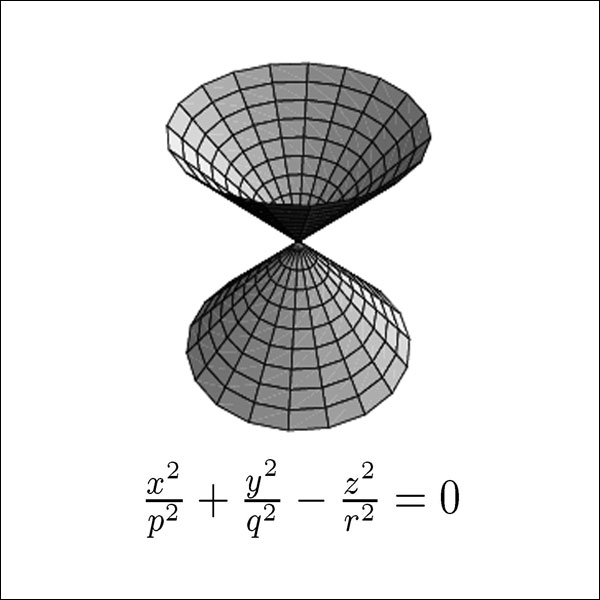
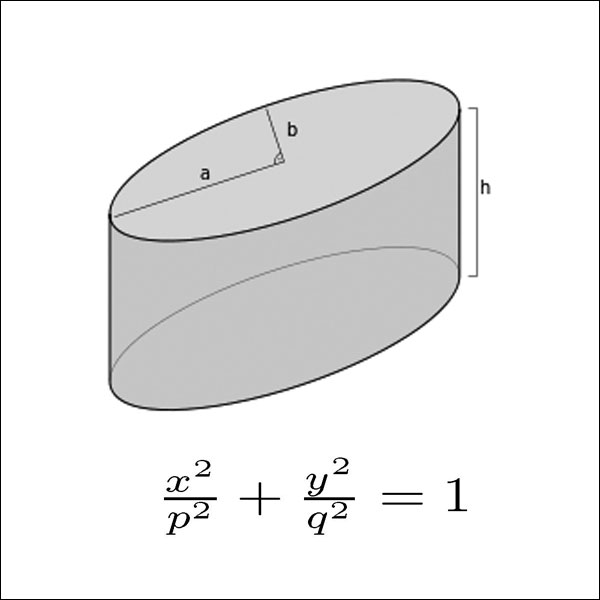
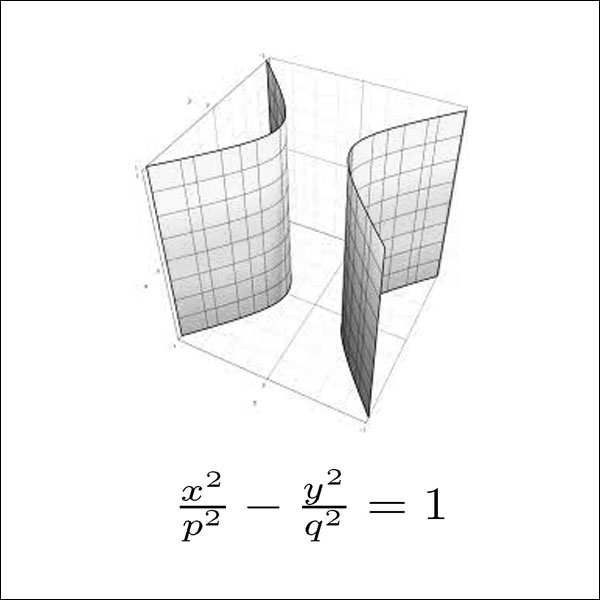
جهت دانلود کتاب هندسه دیفرانسیل مقدماتی Andrew Pressley بر روی لینک زیر کلیک کنید.