حد و پیوستگی توابع

ریاضیات از جمله دروسی است که مباحث آن زنجیروار به هم متصل و با هم مرتبط هستند. مثلا؛ پیشنیاز درک مفهوم انتگرال، مبحث مشتق است و درک مبحث مشتق نیاز به داشتن آگاهی لازم در مورد پیوستکی توابع دارد همچنین برای درک مبحث پیوستگی نیاز به دانستن مفهوم حد توابع است.

در این مقاله و در ابتدا قصد داریم به بیان مفهوم حد تابع و ارائه مثال هایی در این زمینه و نیز قوانین محاسبه برخی حد ها بپردازیم همچنین در ادامه مقاله، پیوستگی توابع و قوانین حاکم بر آن را شرح میدهیم و نهایتا حد و پیوستگی را برای توابع دو متغیره و بالاتر را تشریح میکنیم.

حد تابع یک متغیره

فرض کنید \(f\left( x \right)\) تابعی حقیقی و \(c\) عددی حقیقی باشد، عبارت

\(\mathop {\lim }\limits_{x \to c} f\left( x \right) = L\)

بدین معنا است که اگر \(x\) به اندازه ی کافی به \(c\) نزدیک شود \(f\left( x \right)\) به اندازه دلخواه به \(L\) نزدیک خواهد شد. در واقع می گوییم حد \(f \) وقتی \(x\) به \(c\) نزدیک می شود برابر \(L\) است.

تعریف فوق به صورت ریاضی، درسده ۱۹ توسط کوشی و کارل وایراشتراس بیان شد که به تعریف \(\left( {\varepsilon ,\delta } \right)\) معروف است. در این تعریف \(\varepsilon \) برای نشان دادن یک مقدار مثبت بینهایت کوچک بکار میرود.

به ازای هر \(\varepsilon \) (اپسیلون)، یک \(\delta\) (دلتا) وجود دارد که اگر فاصله ی \(x\) از \(c\) کمتر از \(\delta\) باشد آنگاه فاصله ی \(f\left( x \right)\) از حد تابع کمتر از \(\varepsilon \) شود.

\(\forall \varepsilon > 0,\exists \delta > 0;\left| {x – c} \right| < \delta \to \left| {f\left( x \right) – L} \right| < \varepsilon \)

شکل زیر تعریف فوق را به درستی نشان می دهد.

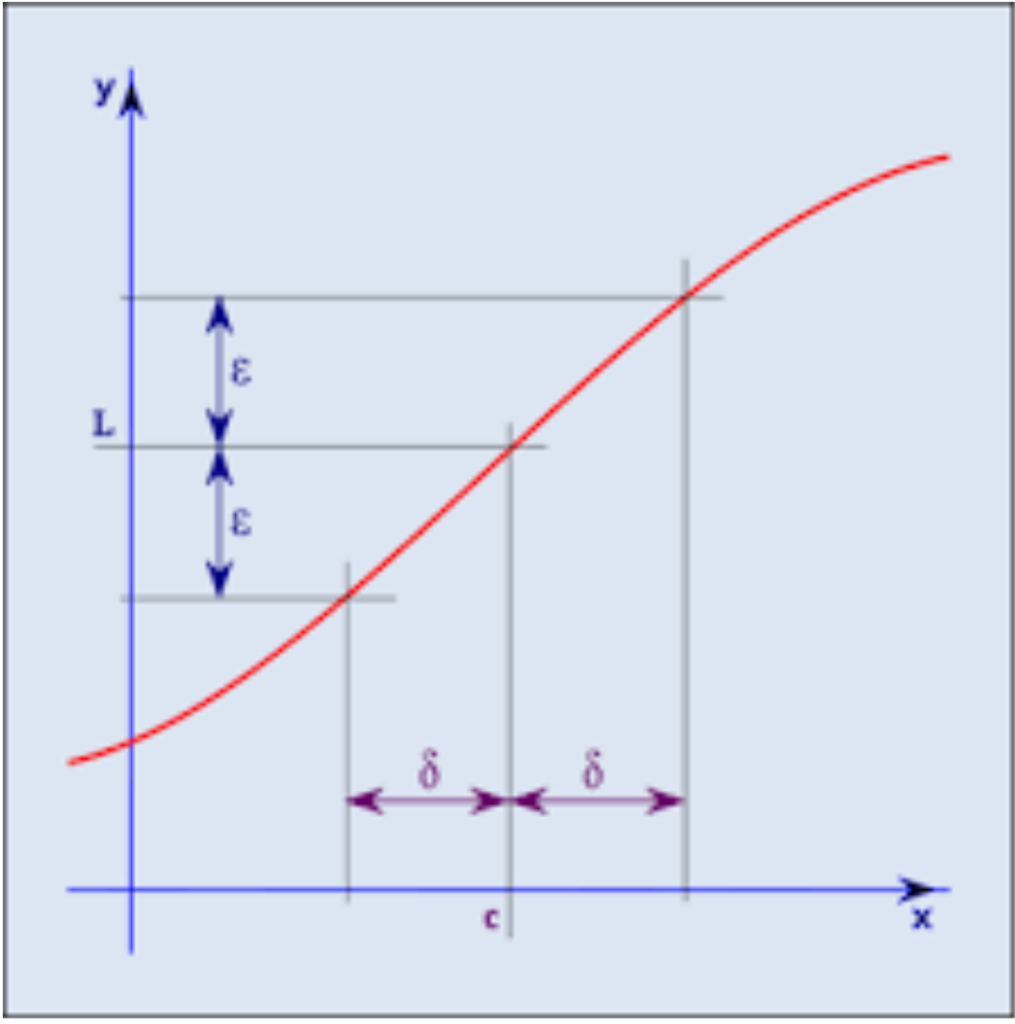
بنابراین اگردر جایی مطرح شد حد تابع در نقطه ای برابر با مقداری مشخص است برای اثبات آن از تعریف حد تابع استفاده کنید بدین صورت که رابطه ریاضی فوق را نوشته و سعی کنیم رابطه ای بین \(\varepsilon \) و \(\delta\) پیدا کنیم.

مثال: به کمک تعریف توابع ثابت کنید که \(\mathop {\lim }\limits_{x \to 2} {x^2} = 4 \).

حل: ابتدا می نویسیم

\(\forall \varepsilon > 0,\exists \delta > 0;\left| {x – c} \right| < \delta \to \left| {f\left( x \right) – L} \right| < \varepsilon \)

حال باید رابطه \(\left| {{x^2} – 4} \right| < \varepsilon \) را باز کرده تا به رابطه ای مشابه رابطه \(\left| {x – c} \right| < \delta \) برسیم و از مقایسه ی این دو رابطه به ارتباط بین \(\varepsilon \) و \(\delta\) برسیم. نتیجه همان دلتایی خواهد بود که در تعریف ریاضی حد توابع دنبال آن می گشتیم.

\(\left| {{x^2} – 4} \right| < \varepsilon \to \left| {\left( {x – 2} \right)\left( {x + 2} \right)} \right| < \varepsilon \to \left| {x – 2} \right| < \frac{\varepsilon }{{\left| {x + 2} \right|}}\left| {x – 2} \right| < \frac{\varepsilon }{4}\)

بنابراین از مقایسه ی رابطه ی \(\left| {x – 2} \right| < \frac{\varepsilon }{4}\) و \(\left| {x – 2} \right| < \delta \) به این نتیجه می رسیم که \(\delta < \frac{\varepsilon }{4}\).

محاسبه ی حد توابع

یکی از عواملی که می تواند به محاسبه دقیق تر توابع کمک کند بدست آوردن حد توابع در نقطه است. لذا لازم است قواعد و دستور العمل هایی برای حد توابع وجود داشته باشد. برخی از این قواعد و قضایا را به طور شهودی در زیر بیان می کنیم.

قضایایی در مورد حد توابع یک متغیره

1- قضیه ی حد مجموع 2- قضیه ی حد حاصلضرب 3- قضیه ی حد تفاضل 4- حد خارج قسمت دو تابع 5- قضیه ی حد تابع مرکب

اگر داشته باشیم \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = {L_1}\) و \(\mathop {\lim }\limits_{x \to a} g\left( x \right) = {L_2}\) آنگاه؛

1- قضیه ی حد مجموع

حد مجموع دو تابع برابر است با مجموع حدهای دو تابع به شرطیکه دو تابع حد داشته باشد.

\(\mathop {\lim }\limits_{x \to a} \left( {f\left( x \right) + g\left( x \right)} \right) = \mathop {\lim }\limits_{x \to a} f\left( x \right) + \mathop {\lim }\limits_{x \to a} g\left( x \right) = {L_1} + {L_2}\)

2- قضیه ی حد حاصلضرب

حد حاصلضرب دو تابع برابر است با حاصلضرب حدهای دو تابع به شرطیکه دو تابع حد داشته باشد.

\(\mathop {\lim }\limits_{x \to a} \left( {f\left( x \right).g\left( x \right)} \right) = \mathop {\lim }\limits_{x \to a} f\left( x \right).\mathop {\lim }\limits_{x \to a} g\left( x \right) = {L_1}.{L_2}\)

3- قضیه ی حد تفاضل

حد تفاضل دو تابع برابر است با تفاضل حدهای دو تابع به شرطیکه دو تابع حد داشته باشد.

\(\mathop {\lim }\limits_{x \to a} \left( {f\left( x \right) – g\left( x \right)} \right) = \mathop {\lim }\limits_{x \to a} f\left( x \right) -\mathop {\lim }\limits_{x \to a} g\left( x \right) = {L_1} – {L_2}\)

4- قضیه ی حد خارج قسمت

حد خارج قسمت دو تابع برابر است با خارج قسمت حدهای دو تابع به شرطیکه حد مخرج به صفر میل نکند.

\(\mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{\mathop {\lim }\limits_{x \to a} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to a} g\left( x \right)}} = \frac{{{L_1}}}{{{L_2}}}\)

---

در ادامه نیز، قضایایی دیگر در مورد حد ذکر می کنیم که یادگیری آن در حل سوالات کمک کننده می باشد.

1- اگر \(f\left( x \right) = c\) که c یک عدد ثابت است آنگاه \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = c\).

2- اگر \(f\left( x \right) = mx + n\) باشد آنگاه

\(\mathop {\lim }\limits_{x \to a} mx + n = ma + n\)

3- اگر \(P\left( x \right)\) یک چند جمله ای باشد آنگاه در هر نقطه دارای حد است و داریم \(\mathop {\lim }\limits_{x \to a} P\left( x \right) = P\left( a \right)\).

4- در محاسبه ی حد اولین قدم جایگذاری است.

5- توابع \(f\left( x \right) = \sin x\) و \(g\left( x \right) = \cos x\) در هر نقطه دارای حد هستند لذا داریم

\(\mathop {\lim }\limits_{x \to a} \sin x = \sin a,\mathop {\lim }\limits_{x \to a} \cos x = \cos a\)

6- تابع \(f\left( x \right) = \tan x\) در هر نقطه ای به جز \(x = k\pi + \frac{\pi }{2}\) دارای حد است لذا داریم

\(\mathop {\lim }\limits_{x \to a} \tan x = \tan a\)

7- تابع \(g\left( x \right) = \cot x\) در هر نقطه ای به جز\(x = k\pi \) دارای حد است لذا داریم

\(\mathop {\lim }\limits_{x \to a} \cot x = \cot a\)

8- اگر c یک عدد ثابت و \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = {L_1}\) و \(\mathop {\lim }\limits_{x \to a} g\left( x \right) = {L_2}\)باشد در اینصورت داریم

\(\mathop {\lim }\limits_{x \to a} cf\left( x \right) = c{L_1}\) \(\mathop {\lim }\limits_{x \to a} {\left( {f\left( x \right)} \right)^n} = {L_1}^n\) \(\mathop {\lim }\limits_{x \to a} \sqrt[n]{{f\left( x \right)}} = \sqrt[n]{{{L_1}}}\)

اگر n را در نظر بگیریم بایستی \({L_1} \ge 0\) باشد.

\(\mathop {\lim }\limits_{x \to a} \left| {f\left( x \right)} \right| = \left| {\mathop {\lim }\limits_{x \to a} f\left( x \right)} \right| = \left| {{L_1}} \right|\)

همچنین

\(\mathop {\lim }\limits_{x \to a} f{\left( x \right)^{g\left( x \right)}} = {\left( {\mathop {\lim }\limits_{x \to a} f\left( x \right)} \right)^{\mathop {\lim }\limits_{x \to a} g\left( x \right)}} = {L_1}^{{L_2}}\)

تعمیم قوانین حد بر روی توابع

تمام قوانینی که برای حد مطرح شد برای حدهای یکطرفه(راست و چپ) نیز قابل تعمیم است.

توجه: اگر تابع داده شده دارای جزصحیح باشد برای محاسبه حد تابع در یک نقطه ابتدا باید جز صحیح را تعیین مقدار کرده و جایگزین کنیم همچنین اگر تابع داده شده دارای قدر مطلق باشد ابتدا باید قدر مطلق را تعییین علامت نموده و قدرمطلق را حذف نموده، سپس حد را محاسبه کنیم.

تابع یک متغیره در چه نقاطی حد ندارد؟

1- اگر حاصل حد چپ و راست مقدار برابری نباشد. به عنوان مثال تصویر زیر را مشاهده کنید

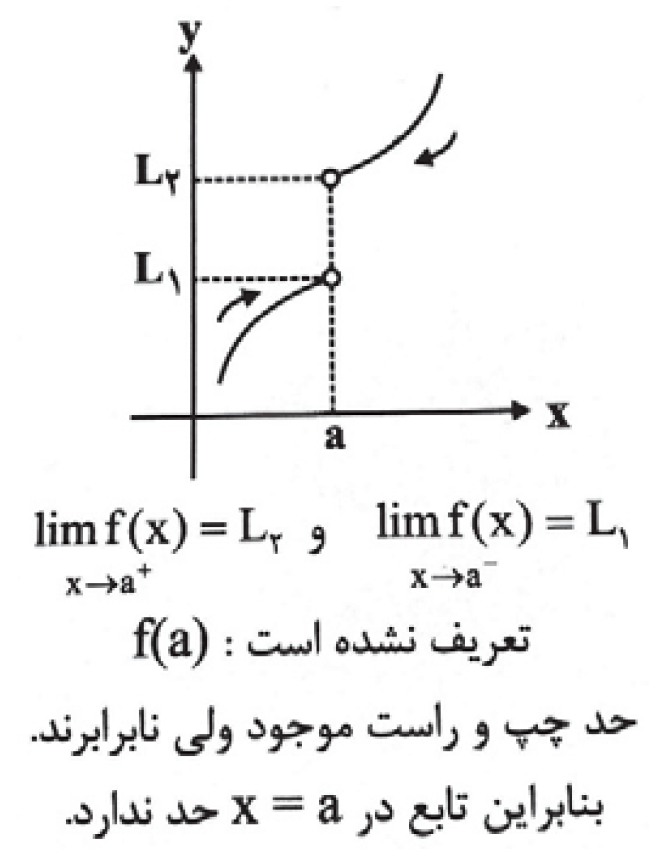
به عنوان مثالی دیگر: حد تابع دوضابطه ای زیر را در نقطه ی \(x = 0\) بررسی می کنیم.

\(\begin{array}{l}
f\left( x \right) = 2x – 1;x \ge 0,\
f\left( x \right) = \sin x;x < 0
\end{array}
\)

برای حل سوال فوق حد چپ و راست تابع f در همسایگی نقطه ی \(x = 0\) را بررسی می کینم.

\(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} 2x – 1 = 2 \times 0 – 1 = – 1
\)

و

\(\mathop {\lim }\limits_{x \to {0^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ – }} \sin x = \sin 0 = 0\)

از اینرو چون حد چپ و راست تابع f موجود اما برابر نیست پس تابع در این نقطه حد ندارد.

محاسبه ی حد به کمک نمودار

برای محاسبه حد راست تابع f در نقطه \(x = a\) ، ازهمسایگی سمت راست بر روی نمودار حرکت کرده تا به نقطه ی \(x = a\) برسیم سپس بر روی محور y ها عمودی رسم می کنیم تا مقدار حد بدست آید. برای محاسبه حد چپ نیز به همین ترتیب عمل میکنیم با این تفاوت که از همسایگی چپ به سمت \(x = a\) بر روی نمودار حرکت می کینم.

حدهای مبهم

گاهی در محاسبه حد توابع کسری با حالت صفر حدی بر روی صفر حدی مواجه می شویم و به اصطلاح گفته می شود حد مبهم است و مقدار حد از روش جایگزینی بدست نخواهد آمد بلکه باید عمال ابهام را از صورت و مخرج حذف کنیم که این عمل رفع ابهام گویند. برای حذف عامل ابهام با توجه به نوع تابع یکی از روشهای زی را به کار می بریم.

1- اگر صورت و مخرج کسری چند جمله ای باشد، صورت و مخرج کسر را تجزیه و سپس ساده کنید.

2- اگر صورت یا مخرج کسری شامل رادیکال با فرجه زوج باشد کسر را گویا کنید. برای اینکار، صورت یا مخرج (یا هر دو) را در مزدوج صورت یا مخرج ضرب نمائید.

3- اگر صورت یا مخرج شامل روابط مثلثاتی باشد از قوانین مثلثاتی استفاده کرده تا عامل ابهام بدست آید و سپس ساده کنید.

توجه: گاهی قبل از رفع ابهام لازم است که متغیر را تغییر داده و متغیر جدیدی تعریف کنیم. لازم به ذکر است که ممکن است متغیر جدید به عدد دیگری میل کند که باید در محاسبه اعمال گردد.

---

در ادامه، مطالب گفته شده در بالا را با ذکر چند مثال روشن می سازیم.

مثال 1: حد \(\mathop {\lim }\limits_{x \to – 2} \frac{{{x^2} + 6x + 8}}{{{x^2} – 4}}\) را محاسبه کنید.

حل:

\(\mathop {\lim }\limits_{x \to – 2} \frac{{{x^2} + 6x + 8}}{{{x^2} – 4}} = \frac{{{{\left( { – 2} \right)}^2} + 6( – 2) + 8}}{{{{\left( { – 2} \right)}^2} – 4}} = \frac{0}{0}\) \(\mathop {\lim }\limits_{x \to – 2} \frac{{{x^2} + 6x + 8}}{{{x^2} – 4}} = \mathop {\lim }\limits_{x \to – 2} \frac{{\left( {x + 2} \right)\left( {x + 4} \right)}}{{\left( {x – 2} \right)\left( {x + 2} \right)}} = \mathop {\lim }\limits_{x \to – 2} \frac{{x + 4}}{{x – 2}} = \frac{{ – 2 + 4}}{{ – 2 – 2}} = – \frac{1}{2}\)

---

مثال 2: \(\mathop {\lim }\limits_{x \to 9} \frac{{2x – 18}}{{\sqrt x – 3}}\)

حل:

\(\mathop {\lim }\limits_{x \to 9} \frac{{2x – 18}}{{\sqrt x – 3}} = \frac{{2\left( 9 \right) – 18}}{{\sqrt 9 – 3}} = \frac{0}{0}\) \(\mathop {\lim }\limits_{x \to 9} \frac{{2x – 18}}{{\sqrt x – 3}} = \mathop {\lim }\limits_{x \to 9} \frac{{2x – 18}}{{\sqrt x – 3}} \times \frac{{\sqrt x + 3}}{{\sqrt x + 3}} = \mathop {\lim }\limits_{x \to 9} \frac{{2\left( {x – 9} \right)}}{{{{\left( {\sqrt x } \right)}^2} – {3^2}}} \times (\sqrt x + 3) = \mathop {\lim }\limits_{x \to 9} \frac{{2\left( {x – 9} \right)}}{{x – 9}} \times (\sqrt x + 3) = \mathop {\lim }\limits_{x \to 9} 2\left( {\sqrt x + 3} \right) = 2\left( {\sqrt 9 + 3} \right) = 12\)

---

مثال 3: \(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {{x^2} + 5} – 3}}{{x – 2}}\)

حل:

\(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {x^2 + 5} – 3}}{{x – 2}} = \frac{{\sqrt {2^2 + 5} – 3}}{{2 – 2}} = \frac{{\sqrt 9 – 3}}{{2 – 2}} = \frac{0}{0}\) \(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {{x^2} + 5} – 3}}{{x – 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {{x^2} + 5} – 3}}{{x – 2}} \times \frac{{\sqrt {{x^2} + 5} + 3}}{{\sqrt {{x^2} + 5} + 3}} = \frac{{{{\left( {\sqrt {{x^2} + 5} } \right)}^2} – {3^2}}}{{\left( {x – 2} \right)(\sqrt {{x^2} + 5} + 3)}} = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 5 – 9}}{{\left( {x – 2} \right)\left( {\sqrt {{x^2} + 5} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} – 4}}{{\left( {x – 2} \right)\left( {\sqrt {{x^2} + 5} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x – 2} \right)\left( {x + 2} \right)}}{{\left( {x – 2} \right)\left( {\sqrt {{x^2} + 5} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{x + 2}}{{\sqrt {{x^2} + 5} + 3}}\) \({\rm{ = }}\frac{{{\rm{2 + 2}}}}{{\sqrt {{\rm{2}}^{\rm{2}} + 5} + 3}} = \frac{4}{{3 + 3}} = \frac{2}{3}\)

---

مثال 4: \(\mathop {\lim }\limits_{x \to 0} \frac{{1 – \cos x}}{{x^2 }}\)

حل:

\(\mathop {\lim }\limits_{x \to 0} \frac{{1 – \cos x}}{{{x^2}}} = \frac{{1 – \cos 0}}{{{0^0}}} = \frac{0}{0}\) \(\mathop {\lim }\limits_{x \to 0} \frac{{1 – \cos x}}{{{x^2}}} = \mathop {\lim }\limits_{x \to 0} \frac{{1 – \cos x}}{{{x^2}}} \times \frac{{1 + \cos x}}{{1 + \cos x}} = \mathop {\lim }\limits_{x \to 0} \frac{{1 – {{\cos }^2}x}}{{{x^2}}} \times \frac{1}{{1 + \cos x}} = \mathop {\lim }\limits_{x \to 0} \frac{{{{\sin }^2}x}}{{{x^2}}} \times \frac{1}{{1 + \cos x}} = 1 \times \frac{1}{{1 + \cos 0}} = \frac{1}{2}\)

---

نکته: رابطه روبرو همواره برقرار است. \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\)

از تساوی فوق روابط زیر نتیجه می شود

\(\mathop {\lim }\limits_{u \to 0} \frac{u}{{\sin u}} = 1\),

\(\mathop {\lim }\limits_{u \to 0} \frac{u}{{\tan u}} = 1\),

\(\mathop {\lim }\limits_{u \to 0} \frac{{\tan u}}{u} = 1\),

\(\mathop {\lim }\limits_{u \to 0} \frac{{\sin u}}{u} = 1\),

تابع پیوسته یک متغیره

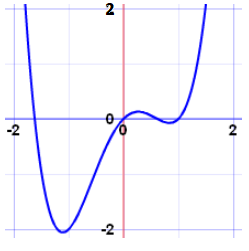
ابتدا برای تعریف تابع پیوسته، از منحنی تابع کمک می‌گیریم. اگر هنگام رسم منحنی تابع \(f(x)\) در هر بازه ای از دامنه اش، هیچ انقطاعی وجود نداشته باشد و نمودار تابع بدون نقطه پرش باشد، \(f(x)\) را پیوسته می‌گویند. البته این توضیح می‌تواند یک تعریف غیر رسمی برای پیوستگی باشد ولی کمک می‌کند که ایده اصلی را درک کنیم. همچنین در توابع پیوسته حد تابع در هر نقطه با مقدار تابع در آن نقطه برابر و یکسان می‌باشد. در تصویر زیر، منحنی یک تابع پیوسته دیده می‌شود.

این تابع می‌تواند یک چندجمله‌ای درجه ۴ باشد به شکل \(f(x) = a{x^4} + b{x^3} + c{x^2} + dx + e\) باشد زیرا در چهار نقطه محور افقی را قطع کرده است، یعنی چهار ریشه دارد. طبق یک قاعده کلی، چندجمله‌ای‌ها، پیوسته هستند.

با استفاده از تعریف ارایه شده در بالا، شاید شناسایی «توابع گسسته» (Discontinues) راحت باشد. به این ترتیب تابع گسسته، تابعی خواهد بود که نمودار آن دارای انقطاع، بریدگی و یا پرش باشد. در نتیجه برای شناسایی چنین توابعی باید به دنبال نقاط انفصال بریدگی و یا پرش باشیم. نمودار توابع زیر پیوسته نیستند و دارای یک نقطه «انفصال» (Hole)، «پرش» (Jump) یا «خط مجانبی عمودی» (Vertical Asymptotic) هستند. در اینجا منظورمان از بریدگی همان خط مجانبی عمودی است.

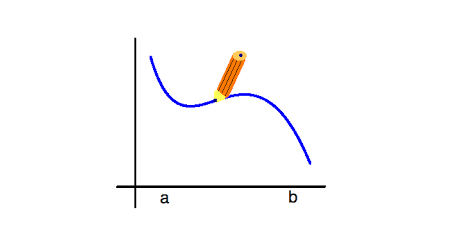
در تعریف هندسی می گوییم، تابعی پیوسته‌ است که بتوان نمودار آن را بدون برداشتن قلم از روی کاغذ رسم کرد.

تابع f در نقطه \(x = a\) پیوسته است هرگاه سه شرط زیر برقرار باشد:

1- \(f(a)\) موجود و متناهی باشد یعنی تابع در نقطه a تعریف شده باشد.

2- حد تابع در نقطه ش موجود باشد یعنی حد چپ و راست موجود و برابر باشد.

3- حد تابع برابر مقدار تابع باشد.

به بیان ریاضی؛ تابع f در نقطه \(x = a\) پیوسته است اگر

\(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = \mathop {\lim }\limits_{x \to {a^ – }} f(x) = \mathop {\lim }\limits_{x \to a} f(x) = f(a)\)

مثال. مقدار x را طوری بیابید که تابع روبرو در آن پیوسته باشد. \(g\left( x \right) = \frac{{{x^2} – 4}}{{x – 2}}\)

حل: نمودار تابع در زیر رسم شده است.

تابع g در \(x = 2\) ناپیوسته است چون در آن نقطه تعریف نشده است( یعی نقطه ی \(x = 2\) جزء دامنه تابع نیست).

پیوستگی در یک فاصله

پیوستگی در یک فاصله را به یکی از حالت های زیر تعریف می کنیم.

تعریف 1: تابع \(y = f\left( x \right)\) را در فاصله ای مانند \(\left[ {a,b} \right]\) پیوسته گویند هرگاه

الف) در تمام نقاط فاصله ی \(\left( {a,b} \right)\) پیوسته باشد.

ب) در نقطه ی \(x = a\) پیوستگی راست داشته باشد.

ج) در نقطه ی \(x = b\) پیوستگی چپ داشته باشد.

تعریف2. تابع \(y = f\left( x \right)\) را در فاصله ای مانند \(\left[ {a,b} \right)\) پیوسته گویند هر گاه

الف) در تمام نقاط فاصله ی \(\left( {a,b} \right)\) پیوسته باشد.

ب) در نقطه ی \(x = a\) پیوستگی راست داشته باشد.

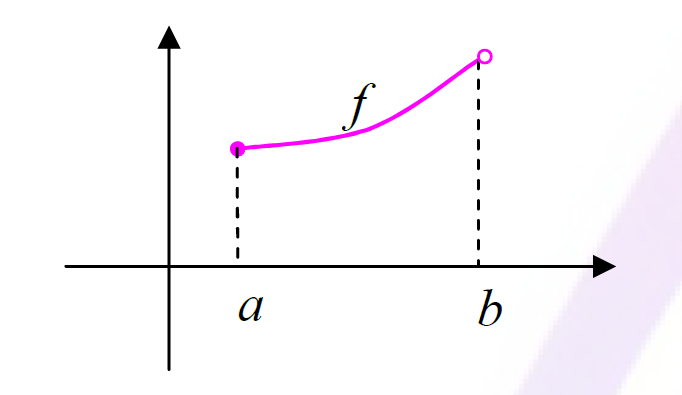
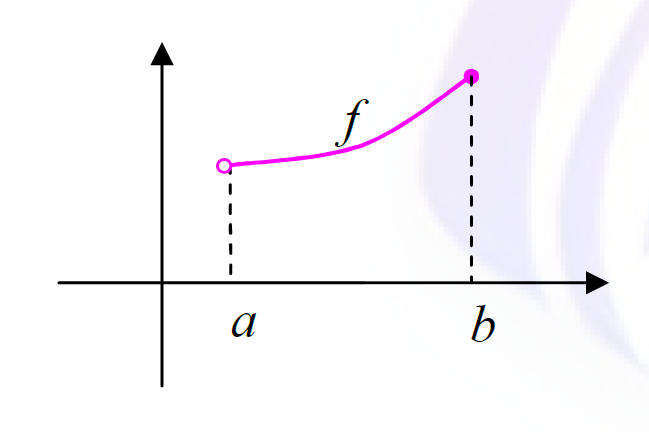
تعریف3. تابع \(y = f\left( x \right)\) را در فاصله ای مانند \(\left( {a,b} \right]\) پیوسته گوییم هرگاه

الف) در تمام نقاط فاصله ی \(\left( {a,b} \right)\) پیوسته باشد.

ب) در نقطه ی \(x = b\) پیوستگی چپ داشته باشد.

تعریف4. تابع \(y = f\left( x \right)\) را در فاصله ای مانند \(\left( {a,b} \right)\) پیوسته گویند هرگاه در تمام نقاط این فاصله پیوسته باشد.

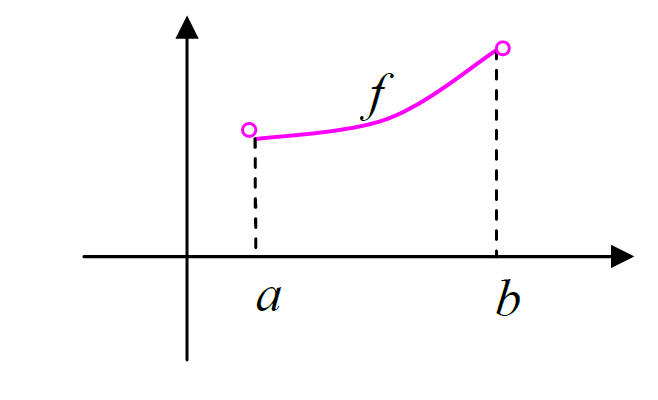
مثال: پیوستگی تابع \(f\left( x \right) = \left[ x \right]\) را در فاصله ی \(\left[ {1,2} \right)\) بررسی کنید.

حل:

ابتدا ثابت می کنیم که تابع در نقطه ی \(x = 1\) پیوستگی راست دارد.

\(\begin{array}{l}
f\left( 1 \right) = \left[ 1 \right] = 1 \
\mathop {\lim }\limits_{x \to 1^ + } f\left( x \right) = \left[ {1^ + } \right] = 1 \
\end{array}\)

بنابراین تابع در نقطه ی \(x = 1\) پیوستگی راست دارد. حال نشان می دهیم که تابع در تمام نقاط فاصله ی \(\left( {1,2} \right)\) پیوسته است. \(a \in \left( {1,2} \right)\) را در نظر می گیریم از اینرو \(\left[ a \right] = 1\).

\(f\left( a \right) = \left[ a \right] = 1\),

\(\mathop {\lim }\limits_{x \to a^ + } f\left( x \right) = \left[ {a^ + } \right] = 1\),

\(\mathop {\lim }\limits_{x \to a^ – } f\left( x \right) = \left[ {a^ – } \right] = 1\),

لذا؛ تابع در تمام نقاط فاصله ی \(\left( {1,2} \right)\) پیوسته است.

مثال: پیوستگی تابع \(f\left( x \right) = 2x + \sqrt {2 – x} \) را در فاصله ی \(\left( {1,2} \right]\) بررسی کنید.

حل:

ابتدا باید ثابت کنیم تابع در نقطه ی \(x = 2\) پیوستگی چپ دارد.

\(f\left( 2 \right) = 2(2) + \sqrt {2 – 2} = 4\),

\(\mathop {\lim }\limits_{x \to 2^ – } f\left( x \right) = 2(2) + \sqrt {2 – 2} = 4\),

بنابراین تابع در نقطه ی \(x = 2\) پیوستگی چپ دارد. حال نشان می دهیم که تابع در تمام نقاط فاصله ی \(\left( {1,2} \right)\) پیوسته است. \(a \in \left( {1,2} \right)\) را در نظر می گیریم از اینرو

\(f\left( a \right) = 2a + \sqrt {2 – a} \),

\(\mathop {\lim }\limits_{x \to a^ + } f\left( x \right) = 2a + \sqrt {2 – a} \),

\(\mathop {\lim }\limits_{x \to a^ – } f\left( x \right) = 2a + \sqrt {2 – a} \),

لذا؛ تابع در تمام نقاط فاصله ی \(\left( {1,2} \right)\) پیوسته است.

خواص توابع پیوسته یک متغیره

خواص زیر برای توابع پیوسته از تعریف پیوستگی و خواص متناظر آن بدست می آید.

1- تابع ثابت \(f\left( x \right) = c\) همه جا پیوسته است.

2- تابع همانی \(f\left( x \right) = x\) همه جا پیوسته است.

3- تابع چندجمله ای \(y = p(x)\) در تمام مقادیر x پیوسته است.

4- تابع \(R\left( x \right) = \frac{{p\left( x \right)}}{{q\left( x \right)}}\) در تمام مقادیری که \(q\left( x \right) \ne 0\) پیوسته است.

کاربرد پیوستگی

توابع پیوسته ویژگی های بسیاری دارند و دلیل اهمیت بالای آن اینست که در ریاضیات کاربردی و رشته های کاربردی از اهمیت بسزایی برخوردارند.

1- هر تابع پیوسته، مشتق تابع دیگری می باشد. به عنوان مثال تابع سرعت و مکان یک جسم متحرک را در نظر بگیرید در اینصورت اگر تابع سرعت جسم متحرک یعنی \(V(t)\) تابع پیوسته ای از زمان باشد آنگاه تابع \(X(t)\) به عنوان فرمولی برای مکان جسم بدست خواهد آمد.

2- کاربرد تابع پیوسته در قضیه مقدار میانی. اگر تابع f روی بازه ی \(\left[ {a,b} \right]\) پیوسته باشد آنگاه به ازای هر N بین \(f(a)\) و \(f(b) \) حداقل یک عدد مانند c در بازه ی \(\left[ {a,b} \right]\) وجود دارد به قسمی که \(f(c) = N\) . در حالتی دیگر از این قضیه داریم: اگر f تابعی پیوسته روی بازه ی \(\left[ {a,b} \right]\) باشد و داشته باشیم \(f\left( a \right)f\left( b \right) < 0\) آنگاه حداقل یک مقدار مانند \(c \in \left[ {a,b} \right]\) وجود دارد به طوری که \(f\left( c \right) = 0\) .

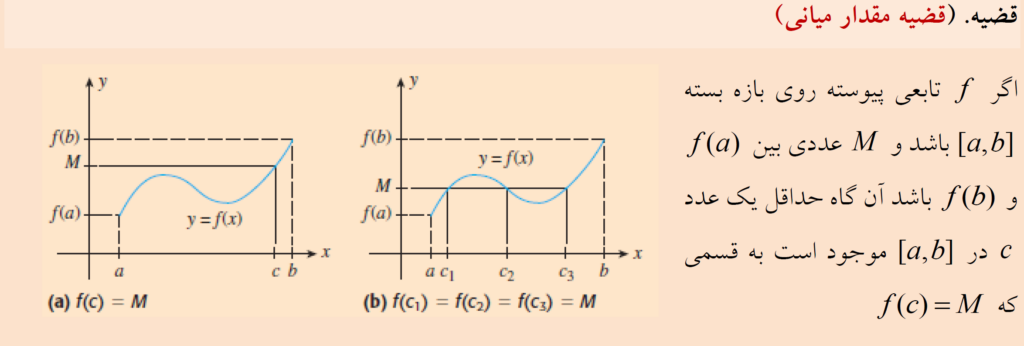
ضروریست هنگام استفاده از قضیه ی مقدار میانی توجه کنید که تابع f پیوسته باشد اگر f پیوسته نباشد ممکن است نتیجه قضیه ی مقدار میانی برقرار نباشد.

قضیه بعد نتیجه ای از قضیه مقدار میانی است. این قضیه نه تنها به ما میگوید که چه وقت تابع f دارای صفر است. (ریشه های معادله \(f(x) = 0\) را صفرهای تابع f می گویند) بلکه روشی اساسی برای تقریب آن بدست می دهد.

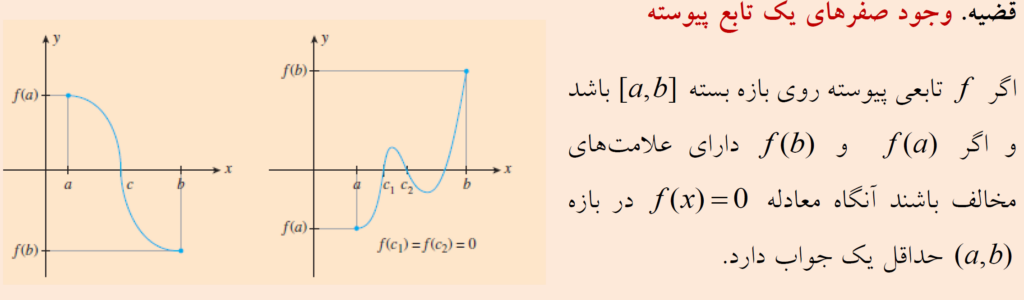
از نظر هندسه این خاصیت بیان می کند که اگر نمودار تابعی پیوسته از بالای محور x به پایین محورx عبور کند یا برعکس، باید از محور x عبور کند. این نکته وقتی تابع f پیوسته نیست لزوما اتفاق نمی افتد.

حد و پیوستگی توابع چند متغیره

تا اینجا، حد و پیوستگی توابع یک متغیره را آموختیم در ادامه حد و پیوستگی توابع دو متغیره را خواهیم آموخت.

فرض کنید می خواهیم حد تابع دو متغیره \(f\left( {x,y} \right)\) را در نقطه ی \(\left( {a,b} \right)\) محاسبه کنیم. در این صورت مسیرهای زیادی برای رسیدن به نقطه ی مورد نظر وجود دارد. به شکل زیر توجه نمائید.

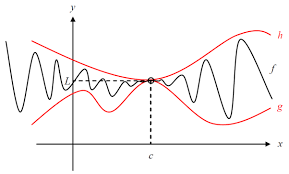
معمولا حد تابع دو متغیره \(f\left( {x,y} \right)\) در نقطه ی \(\left( {a,b} \right)\) به صورت زیر نمایش می دهند.

\(
\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {a,b} \right)} f\left( {x,y} \right)
\)

حاصل حد در تمام مسیرها باید با یکدیگر برابر باشد. همچنین باید توجه داشت که برای برقراری حد لازم نیست که تمامی مسیرها چک شود.

تابع دو متغیره \(f\left( {x,y} \right)\) در نقطه ی \(\left( {a,b} \right)\) پیوسته هست هر گاه؛

\(
\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {a,b} \right)} f\left( {x,y} \right) = f\left( {a,b} \right)
\)

مثال: حاصل حد \(\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{x^2 y^2 }}{{x^4 + 3y^4 }}\) را به دست آورید.

حل:

با جایگذاری نقطه ی \(\left( {0,0} \right)\) در تابع، کسر به صورت \(\frac{0}{0}\) در می آید که باید رفع ابهام نمود و از آنجاییکه رفع ابهام این کسر به علت عدم امکان فاکتورگیری قابل انجام نیست بنابراین حاصل حد رو در مسیرهای مختلف محاسبه می کنیم. باید توجه کنید که تمام مسیر ها باید از نقطه ی \(\left( {0,0} \right)\) بگذرد. اگر پاسخ حد در دو مسیر متفاوت، مقادیر مختلفی باشد تابع در نقطه ذکر شده دارای حد نیست و اگر تابع در دو مسیر متفاوت دارای حد برابر باشد لزوما دارای حد نیست و بایستی مسیر سوم هم بررسی گردد. با انتخاب مسیر، تابع به صورت تک متغیره در می آید و به راحتی می توان حاصل حد را محاسبه کرد. مسیر اول را محور \(x\) در نظر گرفته و از مسیر در نظر گرفته شده به نقطه ی \(\left( {0,0} \right)\) نزدیک می شویم. در این حالت مقدار حد برابر است با:

\(
\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{x^2 y^2 }}{{x^4 + 3y^4 }} = \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{x^2 \left( 0 \right)^2 }}{{x^4 + 3\left( 0 \right)^4 }} = \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} 0 = 0
\)

مسیر دو را محور \(y\) در نظر گرفته و از آن مسیر به نقطه ی \(\left( {0,0} \right)\) نزدیک می شویم در این حالت نیز حاصل حد برابر است با:

\(
\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{x^2 y^2 }}{{x^4 + 3y^4 }} = \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{\left( 0 \right)^2 y^2 }}{{\left( 0 \right)^4 + 3y^4 }} = \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} 0 = 0
\)

بنابراین اگر روی محورهای x , y حرکت کنیم و به مبدا نزدیک شویم حاصل حد برابر خواهد بود اما همانطور که گفته شد این تابع لزوما دارای حد نیست و میبایست مسیر سومی هم چک شود در اینصورت مسیر \(x=y\) را بررسی می کنیم در این حالت حاصل حد به صورت زیر خواهد بود:

\(
\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{x^2 y^2 }}{{x^4 + 3y^4 }} = \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{x^2 x^2 }}{{x^4 + 3x^4 }} = \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{x^4 }}{{4x^4 }} = \frac{1}{4}
\)

همانطور که در محاسبه حدود ملاحضه کردین در مسیر سوم حاصل حد متفاوت از دو مسیر اول بود لذا تابع در نقطه ی مبدا دارای حد نیست.