مفهوم مشتق و کاربردهای آن

مشتق (Derivative) ایدهی اصلی حساب دیفرانسیل، بخش اول آنالیز ریاضی است که نرخ تغییرات تابع را نشان میدهد. مشتق نیز، نظیر انتگرال، از مسئلهای در هندسه، یعنی یافتن خط مماس در یک نقطه از منحنی ناشی شدهاست.
تاریخچهی مشتق
مفهوم مشتق تا اوائل قرن ۱۷ میلادی، یعنی تا قبل از آن که ریاضیدان فرانسوی، پییر دو فرما (Pierre de Fermat ) به تعیین اکسترمم های چند تابع خاص دست بزند، تنظیم نشده بود. فرما دریافت که خطوط مماس، در نقاطی که منحنی ماکزیمم یا مینیمم دارد، باید از این رو به نظرش رسید که مسئله تعیین نقاط اکسترمم تابع، به حل مسئله ی دیگر، یعنی یافتن مماس های افقی مربوط میشود، تلاش برای حل این مسئله ی کلی تر بود که فرما را به کشف برخی از ایده های مقدماتی مفهوم مشتق هدایت کرد.

در نگاه نخست اینطور به نظر میرسید که بین مسئلهی یافتن مساحت سطح زیر یک نمودار و موضوع تعیین خط مماس بر منحنی در یک نقطه رابطهای وجود ندارد، اما اولین کسی که دریافت این دو مفهومِ به ظاهر دور از هم، در واقع ارتباط نسبتاً نزدیکی با هم دارند آیزاک بارو معلم آیزاک، نیوتون، بوده است.

اما مفهوم مشتق به شکل امروزی آن، نخستین بار در سال ۱۶۶۶ میلادی توسط نیوتون و به فاصلهی چند سال بعد از او، توسط گوتفرید لایبنیتز، مستقل از یکدیگر پدید آمد. این دو دانشمند در ادامهی کار خود، باز هم به طور مستقل، بخش دوم آنالیز ریاضی یعنی حساب انتگرال را عرضه کردند که اساس آن بر عمل انتگرالگیری قرار دارد.
نیوتون از شیوهی استدلال سینماتیک و با دیدگاه فیزیکی به بررسی مشتق پرداخته و از آن برای بدست آوردن سرعت لحظهای استفاده میکرد. اما لایبنیتز با دیدگاهی هندسی، از مشتق برای بدست آوردن ضریب زاویهی مماس در منحنیها استفاده میکرد. هر یک از این دو دانشمند نمادهای جداگانهای را برای نشان دادن مشتق به کار میبردند.
پیشرفت حساب دیفرانسیل و انتگرال در دوران بعد به آگوستَن لویی کوشی، برنهارد ریمان و برادران برنولی، یعنی یاکوب و یوهان، مربوط میشود. گیوم لوپیتال (Guillaume de l’Hôpital)، دانشمند فرانسوی، در سال ۱۶۹۶ نخستین کتاب درسی مربوط به آنالیز ریاضی را با نام «آنالیز بینهایت کوچکها برای بررسی منحنیها» منتشر کرد که در واقع خلاصهای از درسهایی بود که یوهان برنولی به عنوان معلم برای او نوشته بود.
در این کتاب، قاعدهی رفع ابهام در حد، با استفاده از مشتق نیز آمده که به قاعدهی هوپیتال مشهور است ولی در واقع متعلق به یوهان برنولی بودهاست
مفهوم مشتق در شکل خط مماس تاریخ بسیار کهنی دارد و برای هندسهدانان یونانی از جمله اقلیدس، ارشمیدس و آپولونیوس شناختهشده بودهاست. ارشمیدس مفهوم بینهایت کوچک را معرفی کرد، هرچند که این مفهوم برای مطالعهی سطحها و حجمها به کار میرفت و توجهی به مشتقها و مماسها نمیشد.
میتوان بهرهگیری از بینهایت کوچکها برای مطالعهی نرخ تغییرات را در ریاضیات هند از حدود سال ۵۰۰ میلادی مشاهده کرد. آریابهاتا که اخترشناس و ریاضیدان بود، از این مفهوم برای مطالعهی حرکت ماه استفاده کرد. باسکارای دوم توسعهی قابل توجهی در استفاده از بینهایت کوچکها برای محاسبهی نرخ تغییرات ایجاد کرد. میتوان گفت که بسیاری از تعریفهای کلیدی در حساب دیفرانسیل از جمله قضیهی رل، در کارهای او دیده میشود.
شرفالدین طوسی، ریاضیدان ایرانی، نخستین کسی بود که مشتق چندجملهایهای درجه سه را کشف کرد. کتاب فی المعادلات او، مفاهیمی از جمله تابع مشتق و بیشینه و کمینهی منحنی را برای حل معادلات درجه سه که ممکن است جواب مثبت نداشته باشند، توسعه داد.
توسعهی نوین حسابان مدیون آیزاک نیوتن و گوتفرید لایبنیتز است که رویکردهای مستقل و یکسانی را برای مشتقگیری و مشتقات فراهم کردند. نکتهی اصلی که این اعتبار را به آنها داد، قضیهی اساسی حسابان بود که مشتق و انتگرال را به یکدیگر مرتبط میکرد. این قضیه، بسیاری از روشهای پیشین برای محاسبهی سطحها و حجمها را که از دوران ابن هیثم توسعهی چندانی نیافته بودند، منسوخ کرد.
نیوتن و لایبنیتز تحقیقات خود دربارهی مشتق را بر کارهای مهم انجام شده توسط ریاضیدانان پیشین از جمله پیر دو فرما، آیزاک بارو، رنه دکارت، کریستیان هویگنس، بلز پاسکال و جان والیس بنا کردند. نیوتن نخستین کسی بود که از مشتق در فیزیک نظری بهره گرفت. لایبنیتز بسیاری از نمادها را توسعه داد که اکنون نیز به کار میروند.
از سدهی هفدهم میلادی بسیاری از ریاضیدانان در زمینهی مشتق پژوهش کردهاند. در سدهی نوزدهم، ریاضیدانان دیگری از جمله آگوستین لویی کوشی، برنهارت ریمان و کارل وایرشتراس تحقیق در این زمینه را تکمیل کردند. در همین دوره، مشتق به فضای اقلیدسی و صفحهی مختلط تعمیم داده شد.
مشتق تابع
اگر \(\left( {x,f\left( x \right)} \right)\) نقطهای از نمودار تابع \(y = f\left( x \right)\) و \(\left( {x + h,f\left( {x + h} \right)} \right)\) نقطهی دیگری از این نمودار باشد، آنگاه \(\Delta f\left( x \right) = f\left( {x + h} \right) – f\left( x \right)\) و شیب خط قاطع عبارت است از:
\(m = \frac{{\Delta f\left( x \right)}}{{\Delta x}} = \frac{{f\left( {x + h} \right) – f\left( x \right)}}{h}\)کسر فوق خارج قسمت تفاضلی \(f\) در \(x\) نامیده می شود. اگر \(x\) ثابت نگه داشته شود و \(h\) به سمت صفرمیل کند، آنگاه خار ج قسمت تفاضلی \(f\) در \(x\) اگر فقط به \(x\) بستگی داشته باشد به مقداری میل می کند که به آن شیب خط مماس گفته می شود. به عبارت دیگر، حاصل حد زیر در صورت وجود ضریب زاویه ی خط مماس نمودارتابع \(f\) در\(x\) را نتیجه می دهد:
\(f’\left( x \right) = {\lim _{h \to 0}}\frac{{f\left( {x + h} \right) – f\left( x \right)}}{h}\)تعریف مشتق تابع
برای تابع \(f\) که در همسایگی نقطه ی \(a\) تعریف شده است، اگر\(f’\left( x \right) = {\lim _{h \to 0}}\frac{{f\left( {x + h} \right) – f\left( x \right)}}{h}\) وجود داشته باشد \(f\) در \(a\) مشتق پذیر است. این حد یکتا را با \(f’\left( a \right)\) نمایش داده و آن را مشتق تابع \(f\) در نقطه ی \(a\) می نامند.
بر طبق این تعریف، مقدار مشتق برابر نرخ تغییرات مقدار تابع است زمانی که تغییرات مربوط به متغیر مستقل به سمت صفر میل میکند.
با تبدیل \(h\) به \(x – a\) تعریف دوم مشتق به صورت زیر خواهد بود:
\(f’\left( a \right) = {\lim _{x \to a}}\frac{{f\left( x \right) – f\left( a \right)}}{{x – a}}\)نمادهای مشتق
لایبنیتز، نیوتون، لاگرانژ، آربوگاست و اویلر هر یک نماد جداگانهای را برای نمایش مشتق بکار میبردند؛ اما در میان پیشگامان اولیهٔ آنالیز ریاضی، لایبنیتز بیش از هر کس دیگری به اهمیت علامات مناسب پی برده بود. او علامات را با حوصله ی زیادی آزمایش میکرد و با سایر ریاضیدانان مکاتبات بسیاری داشت و از این طریق معایب و محاسن نمادهای مختلف را برای آنها مطرح میساخت.
پیشرفت حساب دیفرانسیل و انتگرال و گسترش ریاضیات نوین تا حدود زیادی بواسطه ی علامتهای پیشرفتهای است که بسیاری از آنها توسط لایبنیتس ابداع شدهاند.
لایبنیتز در سال ۱۶۷۵ میلادی با استفاده از عملگر تفاضلی \(\Delta\) خارج قسمت تفاضلی \(\frac{{f\left( x \right) – f\left( {{x_0}} \right)}}{{x – {x_0}}}\) را به شکل \(\frac{{\Delta y}}{{\Delta x}}\) نوشت و برای مشتق تابع \(f\) در \(x\) نماد \(\frac{{dy}}{{dx}}\) را معرفی کرد که به صورت \(\frac{d}{{dx}}f\left( x \right)\) نیز نوشته می شود. این نماد که نمایش دیفرانسیلی مشتق نامیده می شود، برای نمایش مشتق مراتب بالاتر به شکل \(\frac{{{d^n}}}{{d{x^n}}}f\left( x \right)\) نوشته می شود. با استفاده از این نماد تعریف مشتق به صورت \(\frac{{dy}}{{dx}} = {\lim _{\Delta x \to 0}}\frac{{\Delta y}}{{\Delta x}}\) در می آید.
نیوتون برای نشان دادن مشتق اول از\(\dot y\) و برای مشتق دوم از\(\ddot y\) استفاده میکرد. نمادهای نقطهدار نیوتون در برخی مسائل فیزیکی مانند سرعت و شتاب بکار میروند.
مشتق تابع \(f\) را با \(f’\) نیز می توان نشان داد. ای نماد برآن تاکید دارد که \(f’\) تابع جدیدی است که با مشتقگیری از تابع \(f\) بدست آمدهاست و مقدارش در \(x\) با \(f’\left( x \right)\) نموده میشود. مختصات \(x\) و \(y\) واقع بر نمودار \(f\) با معادله ی \(y = f\left( x \right)\) به هم مربوط میشوند، و علامت \(y’\) نیز برای نمایش \(f’\left( x \right)\) بکار میرود که مقدارش در \(x\) به صورت \({y’_x}\) نوشته میشود.
این نماد در سال ۱۷۷۰ میلادی توسط ژوزف لویی لاگرانژ مورد استفاده قرار گرفت و مشتق مراتب بالاتر را به صورت \(f’\) (مشتق اول)، \(f”\) (مشتق دوم)، \(f”’\) (مشتق سوم)، \({f^{\left( 4 \right)}}\) (مشتق چهارم) …\({f^{\left( n \right)}}\) (مشتق nام) نشان میدهد.
در سال ۱۸۰۰ میلادی نماد دیگری توسط لوییس آربوگاست معرفی شد و توسط لئونارد اویلر مورد استفاده قرار گرفت. این نماد مشتق \(f\) را به شکل \(Df\) نشان میدهد. علامت \(D\) یک عملگر دیفرانسیلی است و این فکر را القا میکند که \(Df\) تابع جدیدی است که با مشتقگیری از \(f\) بدست آمدهاست. مشتق مراتب بالاتر به صورت \({D^n}f\) و مقدار آن در \(f\) به صورت \({D^n}f\left( x \right)\) نوشته میشود.
مباحث مشتق
-
مشتقهای یک طرفه
- مشتق راست، مشتق چپ
-
مشتق پذیری
- تعبیر هندسی مشتق پذیری
- موارد مشتق پذیری ( نقاط ناپیوسته، نقاط زاویه دار، نقاط عطف قائم، نقط بازگشت )
-
دامنهی تابع مشتق
-
مشتق تابع نسبت به تابع
- مشتق توابع پارامتری
- مشتق تابع مرکب
- مشتق توابع زوج و فرد
- پاد مشتق
- مشتق جزئی
- مشتق ضمنی ( استفاده از قاعدهی زنجیرهای، استفاده از مشتق جزئی )
- مشتق جهت دار
- مشتق تابع برداری
- مشتق کل
- مشتق تابع معکوس ( تعبیر هندسی )
-
مشتق مراتب بالاتر
- مشتق \(n\) اُم تعدادی از توابع مهم
- قاعدهی لایبنیتز
-
قضیهی رول
- نتیجهی قضیهی رول، حالت خاص قضیهی رول
-
قضیهی لاگرانژ
- تعبیر هندسی ، تعبیرفیزیکی
-
قضیهی کوشی
-
کاربرد مشتق
- خط مماس و قائم
- آهنگ تغییر( آهنگ تغییر متوسط، آهنگ تغییر لحظهای )
- کمیتهای وابسته
- زاویهی بین دو تابع ( زاویهی بین خط و منحنی، زاویهی بین دو منحنی )
- نقاط بحرانی
- تشخیص یکنوایی تابع
- آزمونهای مشتق ( آزمون مشتق اول، آزمون مشتق دوم )
- جهت تقعر و نقطهی عطف
- قاعدهی هوپیتال
- بهینه سازی
- معادلات دیفرانسیل
-
قواعد مشتق گیری در
- توابع جبری، توابع مثلثاتی، توابع معکوس مثلثاتی، توابع نمایی و لگاریتمی، توابع هذلولی
کاربردهای مشتق
در ادامه مطلب به کاربردهای مشتق در ریاضی، فیزیک، معادلات دیفرانسیل و… می پردازیم.

کاربرد مشتق در بهینه سازی- Optimization
اگر\(f\) تابعی مشتقپذیر در دامنهی ℝ (یا روی یک بازهی باز) باشد و \(x\) یک بیشینه و کمینه موضعی \(f\) باشد، مشتق\(f\) در \(x\) صفر است. نقاطی که در آنها مشتق \(f\) صفر است، نقاط بحرانی یا نقاط مانا نامیده میشوند. برای بررسی وضعیت نقطهی بحرانی، مشتق دوم محاسبه میشود.
این روش، آزمون مشتق دوم نامیده میشود. در روشی دیگر که آزمون مشتق اول نامیده میشود، علامت\(f’\)‘ در دو سوی نقطهی بحرانی بررسی میشود.
غالباً مشتقگیری و تعیین نقاط بحرانی، روش سادهای برای یافتن کمینهها و بیشینههای موضعی است و در بهینهسازی قابل استفاده است. بر پایهی قضیهی مقدار نهایی، یک تابع پیوسته روی یک بازه بسته باید دستکم یک مقدار بیشینه و کمینه داشته باشد. اگر تابع مشتقپذیر باشد، کمینه و بیشینه تنها میتوانند در نقاط بحرانی یا نقاط انتهایی ظاهر شوند.
همچنین در رسم نمودار، از این مفهوم استفاده میشود. پس از به دست آوردن نقاط بحرانی یک تابع مشتقپذیر، میتوان نمودار تقریبی را با بررسی صعودی یا نزولی بودن تابع میان نقاط بحرانی رسم کرد.
در ابعاد بالاتر، نقطه بحرانی تابع اسکالر نقطهای است که گرادیان صفر باشد. آزمون مشتق دوم میتواند برای تحلیل نقاط بحرانی قابل بهرهگیری باشد. به این منظور، مقدارهای ویژهی ماتریس هشین مشتقات جزئی دوم تابع در نقطهی بحرانی محاسبه میشوند.
اگر همهی مقدارهای ویژه مثبت باشند، کمینهی موضعی و اگر همه منفی باشند، بیشینهی موضعی است. اگر برخی مثبت و برخی منفی باشند، نقطهی زینی است و اگر هیچ یک از موارد بالا نباشد (مثلاً برخی از مقدارهای ویژه صفر باشند) آزمون بینتیجه است.
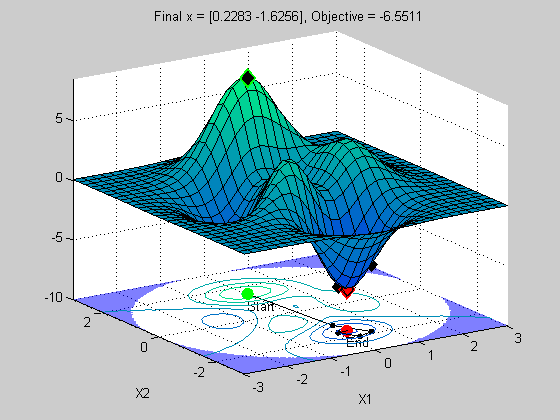
کاربرد مشتق در حساب تغییرات
نمونهای از مسائل بهینهسازی، یافتن کوتاهترین مسیر میان دو نقطه روی یک سطح، با شرط قرار داشتن مسیر روی سطح است. اگر سطح مورد نظر یک صفحه باشد، کوتاهترین مسیر خط راست است. ولی در سطحهای دیگر، نمیتوان کوتاهترین مسیر را به سرعت مشخص کرد.
این مسیرها ژئودزیک نامیده میشوند و یکی از سادهترین مسائل حساب تغییرات، محاسبهی ژئودزیکها است. نمونهی دیگر، یافتن کوچکترین سطح پر شده توسط یک خم بسته در فضا است. این سطح، سطح کمینه نامیده میشود و میتوان آن را با حساب تغییرات محاسبه کرد.
کاربرد مشتق در فیزیک
حسابان در فیزیک دارای اهمیت حیاتی است. بسیاری از فرایندهای فیزیکی با معادلات شامل مشتقات توصیف میشوند و معادلات دیفرانسیل خوانده میشوند. فیزیک به ویژه با تغییرات کمیتها در زمان سر و کار دارد و مفهوم مشتق زمانی (نرخ تغییر در زمان) برای تعریف دقیق چند مفهوم مهم، ضروری است. به طور خاص، مشتقات زمانی موقعیت جسم در فیزیک نیوتنی دارای اهمیت هستند:
- سرعت لحظه ای یک جسم، مشتق جابجایی آن برحسب زمان است.
- شتاب لحظه ای یک جسم، مشتق سرعت آن برحسب زمان و مشتق دوم جابجایی جسم است.
کاربرد مشتق در معادلات دیفرانسیل
معادلهی دیفرانسیل، رابطهای میان مجموعهای از تابعها و مشتقات آنها است. معادلهی دیفرانسیل معمولی گونهای از معادلهی دیفرانسیل است که رابطهی میان تابعهایی از یک متغیر و مشتقات آنها را نشان میدهد. معادلهی دیفرانسیل جزئینوعی معادلهی دیفرانسیل است که رابطهی تابعهایی با بیش از یک متغیر و مشتقات جزئی آنها را بیان میکند. معادلات دیفرانسیل در علوم فیزیکی، مدلسازی ریاضی و ریاضیات دیده میشوند.
کاربرد مشتق در قضیهی مقدار میانگین
قضیهی مقدار میانگین رابطهای میان مقادیر مشتق و مقادیر تابع اصلی را به دست میدهد. اگر\(f\left( x \right)\) تابعی حقیقی باشد و \(a\) و \(b\) دو عدد باشند که a < b، قضیهی مقدار میانگین بیان میکند که شیب میان دو نقطهی \(\left( {a,f\left( a \right)} \right)\) و \(\left( {b,f\left( b \right)} \right)\) برابر با شیب خط مماس بر \(f\) در نقطهای مانند c میان دو نقطهی \(a\) و \(b\) است.
کاربرد مشتق در چند جملهایهای تیلور و سری تیلور
مشتق تابع\(f\left( {{x_0}} \right)\)، بهترین تقریب خطی ممکن آن را در نقطهی دلخواه \({x_0}\) ارائه میدهد؛ ولی این تقریب میتواند بسیار متفاوت از مقدار واقعی باشد. یکی از شیوههای بهبود تقریب، بهرهگیری از تقریب درجه دوم است.
به بیان ریاضی، تقریب خطی تابع حقیقی به صورت \(a + b\left( {x – {x_0}} \right)\) است، در حالی که ممکن است چندجملهای درجه دوم به صورت \(a + b\left( {x – {x_0}} \right) + c{\left( {x – {x_0}} \right)^2}\) تقریب دقیقتری از تابع باشد. با افزایش درجهی چندجملهای میتوان تقریبهای بهتری را نیز به دست آورد. برای این چندجملهایها باید بهترین گزینهی ممکن برای تعیین ضرایب \(a\) و \(b\) و غیره موجود باشد که تقریب را تا جای ممکن بهبود بخشد.
در همسایگی \({x_0}\) ، همواره بهترین تقریب برای \(a\) مقدار تابع \(f\left( {{x_0}} \right)\) و برای\(b\) مقدار\(f’\left( {{x_0}} \right)\) است. برای درجههای بالاتر نیز میتوان این ضرایب را برحسب مشتقات مرتبههای بالاتر\(f\) محاسبه کرد. با این روش میتوان ضرایب چندجملهای تیلور را به دست آورد. قضیهٔ تیلور کران دقیقی را برای کیفیت تقریب میدهد.
حد چندجملهای تیلور در بینهایت، بسط تیلور نامیده میشود. بسط تیلور تقریب بسیار خوبی برای تابع اصلی است. تابعهایی که برابر با بسط تیلور خود هستند، تابع تحلیلی خوانده میشوند. توابع دارای ناپیوستگی یا گوشههای تیز، هرگز نمیتوانند تحلیلی باشند؛ ولی برخی توابع نرم نیز تحلیلی نیستند.




74 Comments
بسیارعالی بود ومتشکرم
البته اینم بگم استاد اون طوری که من فکر میکنم مشتق نوع خاص و حالت خاصی از لیمت است اما شهود و درک کافی نمیتونم از این جمله بگیرم
کاربر محترم، این برداشت و با این بیان صحیح نیست.
توضیحات بیان شده در پاسخ به کامنت قبلیتان را مطالعه بفرمائید و در ادامه، مطلب زیر (تفاوت مشتق و دیفرانسیل)که به کرات در جاهای مختلف از آن صحبت به میان آمده را توجه نمائید.
در ریاضیات متغیر ها قابل شناسایی هستند و میزان تغییر یک متغیر نسبت به دیگری بعنوان مشتق شناخته میشود. معادلاتی که رابطه بین این متغیرها و مشتقات آنها را تعریف میکنند، معادلات دیفرانسیل نامیده میشوند. دیفرانسیل فرآیند یافتن مشتق است. مشتق تابع، میزان تغییر مقدار خروجی نسبت به مقدار ورودی آن است، درحالیکه دیفرانسیل تغییر واقعی تابع است.
موفق و موید باشید.
سلام درود استاد گرامی
دو سوال داشتم اگر لطف کنید پاسخ بدید خیلی ممنون میشم از سایت ها چیزی پیدا نکردم.
اول اینکه تفاوت حد با مشتق چیه ؟
دوم اینکه تفاوت مشتق با دیفرانسیل چی هس ؟
ممنون از سایت خوب شما هر بار که بازش کردم یه مطلب جدید یاد گرفتم امیدوارم برسه بالای سایت ویکی پدیا
سلام بر شما کاربر محترم
دد زیر توضیحاتی رو می نویسم که امیدوارم تفاوت را برایتان روشن سازد.
حدها ابزارهایی در ریاضی هستند در جهت کمک به شما، تا پاسخ این سوال را بدهید که مقدار یک عبارت چقدر خواهد بود وقتی متغیر تشکیل دهنده آن به مقدار مشخصی نزدیک می شود. (دانستن این موضوع نیز بسیار مهم است که در مواردی، متغیر یک عبارت مقادیری را نمی تواند اختیار کند مانند مقدار صفر که نمی تواند در مخرج باشد.)
مشتق ها، آهنگ تغییرات یک عبارت(متغیر وابسته) نسبت به یک متغیر مستقل است. یک روش معمول برای یافتن آهنگ تغییرات اینست که مقدار یک عبارت را در دو نقطه بیابیم و نسبت تفاوت این دو مقدار را بر اختلاف مقادیر دو نقطه مذکور به عنوان متغیر مستقل بدست آوریم. البته اگر سرعت تغییرات یکنواخت نباشد آهنگ تغییرات محاسبه شده می تواند تغییر فیزیکی خاصی داشته باشد. برای مثال در مقوله ی حرکت، اگر تنها سرعت اولیه و سرعت نهایی را بدانیم، برای توصیف بهتر حرکت، دانستن شتاب نیز لازم است. حال اگر بخواهیم جواب روشنی به این مسئله بدهیم(توصیف مسیر حرکت)نیاز داریم که آهنگ تغییرات در دو نقطه را بدانیم چرا که آهنگ تغییرات در نقاط مختلف تغییر میکند(متفاوت است). اما در محاسبات قبلی نیاز داشتیم که دو نقطه مختلف را ببینیم و در آنجا مفهوم حد به کمک می آید زیرا ما می توانیم از مفهوم یک حد وقتیکه دو نقطه را به هم نزدیک می کنیم و به یک نقطه تبدیل می کنیم استفاده کنیم.
آرزوی موفقیت برای شما
سلام و احترام
یک دنیا سپاسگزارم استاد توضیحات جامع و مفیدی بود متوجه شدم
سلام بر شما کاربر گرامی
خواهش میکنم
از اینکه مورد رضایت شما قرار گرفته خرسندم.
موفق باشید
من عدد (f(a رو متوجه نمیشم چه جور بدست میاد.
مثلا a رو ۲ بدیم تو معادله که می خواهیم بدست بیاریم(f(a رو چگونه است؟؟
سلام بر شما کاربر محترم
f(a) یعنی مقدار عددی تابع f در نقطه a. در صورتیکه مقدارa داده شده باشد با جایگذاری مقدار a در تابع داده شده به جای متغیر تابع، مقدار عددی f(a) بدست خواهد آمد.
آرزوی موفقیت برای شما
باسلام خدمت شما میخواستم بپرسم اینکه تابع درداخل بازه مشتق پذیر است درانجام های بازه چرا مشتق پزیرنیست؟
سلام بر شما کاربر محترم
لطفا سوالتان را دقیق و واضح مطرح بفرمائید.
سلام استاد
من ترم اول دانشگاهم این نماد d که در انتگرال و مشتق استفاده میشه رو نفهمیدم چیه
چون در دبیرستان از این نماد استفاده نمیکردیم و به ما که نظام جدید هستن یاد ندادن و الان در دروس دانشگاهی همیشه استفاده میشه که هیچکس هم درست حسابی توضیح نمیده این d از کجا اومده و چه معنی میده
ممنون میشم اگه توضیحش بدین
مثلا d/d(x) چرا به معنی مشتق در نقطه x هست یا انتگرال x^2 d(x) اینحا d(x) چه معنی دارد
سلام بر شما کاربر گرامی
نماد d (مخفف Differential) به معنای تغییرات جزئی یک تابع است وقتی که متغیر مستقل آن تابع تغییر میکند پس میتوان به عنوان مثال نوشت: df/dx که f تابع و x متغیر مستقل تابع f است. انتگرال و مشتق ضد یکدیگرند اگر از یک تابع انتگرال گرفته شود خروجی انتگرال مشتق تابع زیر انتگرال است و بالعکس.
برای اینکه مفهوم d در تعریف انتگرال را متوجه شوید ابتدا باید مفهوم مجموع ریمان را بیاموزید.
مجموع ریمان:
یک منحنی در صفحه xy را در نظر بگیرید به عنوان مثال منحنی نمودار sinx. پیدا کردن مساحت زیر یک نمودار منحنی، کار ساده ای نیست چون سطح زیر منحنی یک شکل منظم نیست پس هیچ فرمول تعریف شده ای برای پیدا کردن مساحت آن وجود ندارد. بنابراین ما باید به دنبال راهی برای حل این مشکل باشیم. از اینرو؛ از تخمین مساحت زیر منحنی به کمک مجموعه ای از مستطیلها استفاده میکنیم. ابتدا محدوده مورد نظر برای محاسبه مساحت زیر منحنی را مشخص میکنیم و آن را به مستطیل هایی با عرض یکسان که آن را دلتا ایکس می نامند تقسیم میکنیم( دلتا ایکس برابر است با xi+1- xi). اگر تعداد مستطیل ها کم باشد مقدار دقیق مساحت زیر منحنی با مقدار محاسبه شده مجموع مساحت مستطیل های رسم کرده با خطا همراه است بنابراین اگر در بازه ذکر شده تعداد مستطیل ها را افزایش دهیم یعنی دلتا ایکس را به سمت صفر میل دهیم در این صورت مقدار دقیق مساحت با مقدار محاسبه شده برابری خواهد کرد.
به مجموع مساحت مستطیل های رسم شده که به صورت زیگما نوشته میشود مجموع ریمان گفته می شود در اینجاست که نماد انتگرال خود را نشان میدهد به این معنا که؛ به جای علامت زیگما از علامت انتگرال که در واقع s کشیده است(یعنی مساحت) و به جای دلتا ایکس از نماد dx استفاده میکنیم.
موفق باشید.
ممنونم استاد متوجه شدم
پس یعنی در واقع d(x) در انتگرال یا مشتق فقط مشخص میکند که متغیر مستقل ما کدوم متغیر است که با تغییرات جزئی اون متغیر مقدار تابع ما تغییر میکند؟
و یعنی در محاسبات در چیزی ضرب یا تقسیم نمیشود و صرفا برای نمایش متغیر مستقل تابع به کار میرود؟
و df/d(x) به این دلیل مشتق تابع در یک نقطه را نشان میدهد که دلتاy تقسیم بر دلتا x شده فقط اون دلتا چون به صفر میل میکنه دیگه اندازه یک نقطه میشه
سلام بر شما کاربر محترم
خواهش میکنم
بله توضیحاتی که نوشتین درستِ
فقط در تکمیل بند آخر اضافه میکنم که df/dx یعنی تغییرات تابع f وقتی x تغییر میکند. حالا میتونه تغییرات ایکس مثبت باشه یا منفی.
موفق باشید.
سلام استاد فرزامی و خیلی ممنون از مطالب مفیدی که گذاشتین
بنظرم جالب میاد که خط مماس غیر عمودی رو بدوناستفاده از مشتق قابل تعریف نیست. از طرفی خط شیب خط مماس عمودی (قایم) هم تعریف نشده است. بنظرتون خط مماس رو چطور تعریف کنیم که هر دو حالت رو شامل بشه؟
سلام بر شما
متشکرم از حسن نظرتون
سوال شما اینه که ما در یک منحنی همزمان هم خط مماس عمودی و هم خط مماس افقی رو داشته باشیم؟
شما دایره رو به صورت دو خم (منحنی) در نظر بگیرید. فرض کنید در خم بالایی بخواهیم شیب خط مماس در هر نقطه رو حساب کنیم با توجه به اینکه خط مماس خطی راست است که در هر نقطه از منحنی آن را لمس میکند(قطع نمیکند).
بنابراین در هر نقطه میتوان یک خط مماس رسم کرد که شیب خط مماس در هر نقطه نسبت به نقطه دیگر متفاوت است.
پس در یک خم، در هر نقطه فقط یک خط مماس وجود دارد و نمیتوان در یک نقطه همزمان هم خط مماس قائم داشت هم افقی.
اندازه شیب خط مماس با استفاده از مشتق محاسبه می گردد.
موفق باشید.
سلام محدد استاد و خیلی ممنونم از پاسختون. منظورم تعریف خط مماس بودش که واسه تعریفش درحالت غیر عمودی بودن خط مماس چاره ای جز استفاده از مشتق نداریم و در حالت عمود بودن خط مماس مثل خط مماس بر نمودار تابع y=x^{1/3} که در مبدا که مشق نداره باستی بدون استفاده از مشتق خط مماس رو معرفی کرد. ی سوال مهم این هستش که خط مماس رو به کمک مشتق تعریف میکنیم یا مشتق رو به کمک خط مماس چون و من فکر میکنم اولی درست هستش. ممنون میشم نظرتو ن رو بدون و نیز تعریف خط مماس رو از نظر شما بدونم
سلام مجدد بر شما
خواهش میکنم
احتراما؛ همونطور که در کامنت قبلی خدمت شما عرض کردم در هر نقطه از یک منحنی در صورت وجود خط مماس، خطوط مماس دارای ضریب زاویه های متفاوت هستند و این یعنی خطوط مماس در هر نقطه با دیگری متفاوت است.
و اما، برای اینکه بررسی کنیم در یک نقطه از منحنی خط مماس وجود دارد یا خیر؟ بایستی ابتدا بررسی کنیم که آیا نقطه مورد نظر جزئی از دامنه تابع (منحنی) ذکر شده هست یا نه؟ اگر جزئی از دامنه بود پیوستگی در آن نقطه را بررسی میکنیم. در صورت پیوسته بودن(که شرط بررسی مشتق پذیری است)، مشتق پذیری تابع در آن نقطه را(از راه تعریف یا فرمول) بررسی می نمائیم اگر مشتق در نقطه مذکور وجود داشته باشه در اینصورت مقدار مشتق در آن نقطه برابر با شیب خط مماس در آن نقطه است و به راحتی میتوان معادله خط مماس را بدست آورد.
اگر مشتق تابع در نقطه مطرح شده موجود نباشد(برابر با مثبت یا منفی بینهایت باشد) در اینصورت خط x=x0, که در راستای قائم است خط مماس بر منحنی در نقطه مورد نظر است.
پس، این نشان می دهد که برای بدست آوردن خط مماس نیاز به بررسی مشتق پذیری است.
در ضمن؛ شیب خط قائم بر منحنی در نقطه مورد سوال، برابر است با قرینه معکوس شیب خط مماس بر منحنی که معادله خط قائم بر منحنی هم براحتی قابل بدست اوردن است.
لازم به ذکر است که بدانید شیب خط قائم بر منحنی در هر نقطه، در صورتی که شیب خط مماس (مقدار مشتق در آن نقطه) مثبت یا منفی بینهایت باشد، برابر صفر است.
آرزوی موفقیت برای شما
سلام. ممنون از توضیحاتتون.
به نظر من اکثر دانش آموزان مشکلشون از پایه و از جایی که حروف انگلیسی وارد ریاضی میشه.
همین که حروف انگلیسی یا انواع فرمول وارد دروس ریاضی میشه همه درس رو سخت میکنه و دل افراد رو میزنم.
من عاشق درس ریاضی هستم. اما فقط از حروف انگلیسی در ریاضی و انواع فرمول متنفرم.
علاقه به تمرین هم ندارم خیلی دوست دارم ذهنی همه ریاضیات رو حساب کنم.
پیچیدگی در انواع نام ها مانند توابع و … هم آدم رو گیج میکنه.
من دانشجو کاردانی مکانیک بودم که امسال مجبور به ترک تحصیل شدم و برام خیلی سخت بود.
سلام بر شما کاربر محترم
ریاضی بدون نمادها (با استفاده از حروف انگلیسی) قابل بیان نیست.
باید بپذیریم که خواندن و یادگیری درس ریاضی منوط به پذیرش نمادهایی هست که در هر مبحثی از آن استفاده شده است.
مباحث ریاضی با فرمول همراه است و فرمول به صورت پارامتری بیان میشود و بعد با اعداد و ارقام جایگذاری میشود.
ذهنی ریاضی حل کردن در حد جمع و تفریق و ضرب و تقسیم و پاره ای از مسائل قابل اجراست و شما باید برای حل مسائل ریاضی از نوشتن استفاده کرده و آنقدر تکرار کنید که فرمول را درک و ملکه ذهنتان گردد.
آرزوی موفقیت برای شما
سلام استاد
میشه درمورد کاربرد مشتق در علوم زیست توضیح بدید برام ممنون میشم
میزنم رو لینک میزنه همچین صفحه ای وجود نداره😟😞
سلام سرکار خانم دکتر فرزامی لطفاً در صورت امکان در مورد رابطه ریاضی سئوال زیر راهنمایی بفرمایید. هرچند در این سئوال نوشتن ۱۳ حالت ممکن ساده است ولی در موارد بزرگتر چه رابطه ریاضی وجود دارد؟
به چند طریق می توان با سکه های ۲۰۰ و ۵۰۰ ریالی ۱۲۰۰۰ ریال تهیه کرد؟
با سپاس
موسویان
در یک مورد به من گفته شده رابطه موجود با استفاده از معادله دو خط و انتگرال گرفتن از ۱۲۰۰۰ برقرار است؟؟؟
سلام بر شما کاربر گرامی
در سوال مطرح شده توسط شما، معادله دیوفانتی زیر رو باید حل نمو و نیازی به انتگرال گیری نیست و ربطی به انتگرال گیری ندارد
. تعداد سکه های ۲۰۰ ریالی را x و تعداد سکه های ۵۰۰ ریالی را y در نظر بگیرید بنابراین با حل این معادله و تعداد جوابهای ثبت پاسخ سوالتون رو دریافت خواهید کرد.
120=2x+5y
آرزوی موفقیت برا شما
سلام من خیلی علاقه به ریاضی دارم اما یاد گرفتن ریاضی برام سخته و اصلن از ریاضی سردر نمیارم.
دلیلش اینکه در دورههای ابتدای و راهنمای به این درس خوب گوش ندادم و سعی نکردم این درس را یاد بگیرم.
حالا که میخوام این درس را یاد بگیرم با مشکلات زیادی روبه رو میشوم.
چه جوری میتونم تو این درس پیشرفت کنم.
لطفاً کمک کنید
سلام به شما کاربر محترم
شما اولین قدم برای یادگیری ریاضی را طبق گفته خودتان دارید که همان علاقه هست.
بدون علاقه نمیشود مطلب یا فن یا کاری را آموخت. اما بعد از علاقه مهم ترین مساله، هدفی است که شما از خواندن و یادگیری این درس انتظار دارید.
هدف را مشخص کرده و پس از آن متناسب با هدف ارزیابی اولیه ای از خودتان نسبت به آموخته هایی که از ریاضی در ذهن دارید داشته باشید و در نهایت اقدام به مطالعه و یادگیری کنید.
فراموش نکنید شرط یادگیری تکرار پذیری و انجام تمرین های متعدد است.
شما میتوانید با درگاه های ارتباطی که در قسمت ارتباط با ما است، سوالات خود در خصوص مشاوره تحصیلی را با ما در میان بگذارید.
آرزوی موفقیت برای شما
سلام
در مورد مشتق کدام کتب جدید را پشنهاد میکنید که ویژهگی زیر در آن موجود باشد.
تشریح موضوعات بصورت مفصل
مثال های حل شده مرتبط به موضوع و وجود مسئله برای خود آزمایی
داشتن تمرینات زیاد
سلام
در مورد مشتق، به سطحی که در آن تحصیل میکنید بستگی دارد.
اگر در سطح دبیرستان بخواهید مطالعه کنید هر کدام از کتابهای مولفین محترم قابلیت های خاص خود را دارد.
(نردبام)خیلی سبز
کتابهای گاج
میکرو طلائی
و…
اگر در سطح دانشگاهی بخواهید مطالعه کنید.
سیلورمن
جورج توماس
سلام و ممنون از توضيحاتتون
ميخواستم بدونم مشتقات جزئى مرتبه دوم يك تابع چند متغيره، مفهوم خاصى را به ما ميدن؟ در مورد ماتريس هسين اطلاع دارم ولى ميخوام بدونم هر كدوم از اعضاى ماتريس هسين آيا به تنهايى مفهوم خاصى دارن؟!
ممنون
سلام بر شما کاربر گرامی
خواهش میکنم تشکر
ببینید قطع به یقین، تمام مباحث ریاضی هم در سطح کاربردی و هم در سطح محض، کاربردیست اگر چه از دیدگاه ما خشک و بلااستفاده به نظر آید.
کلا خاصیت مشتقات مرتبه دوم چه در مورد یک متغیره ها چه در مورد چند متغیره ها اینست که آهنگ تغییر کمیتی مورد نظر در آن تابع را بیان میکند.
به عنوان مثال ساده، فرض کنید معادله حرکت یک جسم را دارید.
آهنگ حرکت این جسم نسبت به زمان، که با مشتق مرتبه دوم نمایش داده میشود بیانگر شتاب حرکت آن جسم است.
از مفهوم مشتق مرتبه دوم نیز می توان برای تعیین تقعر یک جسم استفاده کرد. و…
در رابطه با Hessian Matrix می دانیم که ماتریسی مربعی در بحث توابع چند متغیره هست که کل درایه های آن مشتقات مرتبه دوم تابع مورد نظر است.
مفهوم هر کدام از درایه ها به تنهایی همان مفهوم مشتق مرتبه دوم است.
اما حاصل ماتریس ما را در تعیین انحنای تابع مورد نظر یاری میکند.
وقت بخير خانم فرزامى عزيز و دوستان گرامى
بنده دانشجوى مديريت هستم و به زودى فارغ التحصيل ميشم
ميخواستم بدونم اين مشتق كه توى رياضيات ٢ مفصل ازش صحبت شد
توى مباحث مربوط به ما يعنى مباحث مديريتى چه كاربردى داره
ممنون ميشم اگه به صورت كاربردى به من توضيح بديد يعنى توى موارد مديريتى مشتق چه كمكى ميتونه بكنه
آيدى تلگرام بنده اين هست اگه ممكنه منبعى در اختيار من بزاريد @deiiali
سلام بر شما کاربر گرامی
ببینید در خصوص کاربرد ریاضیات در علوم مختلف همیشه از سمت افراد با تخصص های مختلف سوال های مختلفی مطرح شده است اما هنوز اقدام موثری صورت نگرفته است.
نتیجه اولین کنفرانس ریاضی کاربردی در ایران که در اواخر دهه ۸۰ در دانشگاه سیستان و بلوچستان برگزار شد این بود که ریاضیات به صورت کاربردی و تفکیک شده در علوم مختلف، حداقل ۲۰ سال زمان خواهد برد.
با این حال، کتابهایی ممکن است باشد که کاربرد ریاضیات در مدیریت را تا حدودی نشان دهد.
سلام استاده محترمه اگر ما از یک جسم نطر به چند متغیر مشتق بگیرم جی میشه لطفا معلومات دهید.
سلام به شما کاربرگرامی
سوالتان را دقیق مطرح بفرمایید.
با سلام و عرض ارادت
من یک دانش آموز کنکوریم و اطلاعاتم در حد دبیرستانه لطف میکنید بفرمایید چه زمانی حق نداریم از فرمول های مشتق استفاده کنیم و باید به جاش از تعریف مشتق استفاده کرد و هم چنین در بعضی مسائل کاملا برعکس و باید حتما از فرمول استفاده کرد و به دو جواب متفاوت میرسیم و هردو جواب توی گزینه ها هست که تحملش برام دیوونه کننده شده
فکر میکنم نکته خاصی وجود داره که توی کتاب های من نوشته نشده و من خیلی به اون نکته نیاز دارم
از شما بسیار متشکرم لطف کنید اگر چیزی در این رابطه هست بهم بگید من فرصت زیادی ندارم
با تشکر
با سلام و احترام
هیچ وقت جواب مشتق یک تابع چه با استفاده از تعریف چه با استفاده از فرمول متفاوت نخواهد شد.
در سوال تشریحی بیان میشه که با استفاده از تعریف، مشتق پذیری تابع ذکر شده را بررسی کرده و در صورت وجود مقدار آن را محاسبه کنید.
در سوالات تستی نیز، با توجه به گزینه ها میتوان متوجه شد که استفاده از تعریف مشتق را درگیر باید کرد و یا اینکه باید از طریق فرمول های مشتق، مشتق تابع را بررسی نمود.
سلام میشه بگویند که هدف از قضیه میانگین در مشتق چیست
سلام بر شما کاربر گرامی
همونطور که میدونید قضیه میانگین (Mean Value Theorem) حالت کلی تری از قضیه رول(Roll’s Theorem) هستش و تعمیم آن قضیه کوشی(Cauchy’s theorem) است.
اولین ویژگی تابع مورد بحث در این قضیه پیوستگی آن است.صورت و اثبات هر دو قضیه درکتابهای مختلف ریاضی آمده است.
معمولا بسیاری از قضایا در ریاضیات کاربرد غیر مستقیم دارند و میتوانند در اثبات قضایای دیگر یا مسائل گوناگون کمک کننده باشد.
این قضیه نیز در اثبات قضیه های زیاد و مهمی کاربرد دارد همچنین در آزمون مشتق اول برای بررسی صعودی یا نزولی بودن یک تابع نقش دارند همچنین در اثبات بسیاری از نامساوی ها کاربرد خود را نشان میدهد.
سلام
من دقيقا تفاوت ديفرانسيل و مشتق را مي خواهم بدونم اگر لطف كنيد توضيح دهيد
سلام بر شما کاربر گرامی
تفاوت این دو را در پاسخ به کاربر محترم دیگری قبلا شرح داده ام. اگر پیدا نکردین بفرمائید مجددا خواهم گفت.
سلام
هیچ وبسایتی نیومده بگه مشتق دقیقا چیه
همه دوتا فرمول گذاشتن
تا مفهومش رو ندونم چیه هزار بار هم حفظش کنم باز از یادم می ره و ماندگار نمی شه. مفهومش رو باید برای هر حالتی با رسم شکل نشان داد نه اینکه یه تعریف گنگ تر از خودش بدید.
سلام بر شما کاربر گرامی
به طور کلی، در ریاضیات فراگیری مفهوم یک مبحث نیاز به دانستن و درک خوبی از پیش نیازها داره که متاسفانه بخاطر عدم درک کامل و جامع از پیشنیازها مفهوم مبحث مورد نظر رو نمیشه بدرستی دریافت.
بنابراین در مورد مشتق توصیه میکنم در ابتدا مفاهیم تابع، حد و پیوستگی را بدرستی فرا گیرید.
در ضمن چه در ریاضیات چه در سایر علوم، اینترنت پاسخگوی جامعی برای درک خواسته های شما نخواهد بود و سعی کنید از کتب مختلف کمک بگیرید.
آرزوی موفقیت برای شما
سلام بر شما کاربر گرامی
در ابتدا تشکر میکنم از نقد شما.
اما ضمن احترام به سوال شما اشاره ای میکنم که “عمومیت” دارد.
به طور کلی، در ریاضیات فراگیری مفهوم یک مبحث نیاز به آموزش و درک صحیحی از پیشنیازها دارد که بخاطر عدم آموزش کامل و صحیح از پیشنیازها مفهوم مبحث مورد نظر رو نمیشه بدرستی دریافت.
در پاسخ به خواسته صحبت شما هم، اولا توصیه میکنم(چه در ریاضیات چه در سایر علوم) که چون اینترنت پاسخگوی جامعی برای درک خواسته های شما نخواهد بود سعی کنید از کُتب مختلف کمک بگیرید و در ابتدا مفاهیم تابع، حد و پیوستگی را بدرستی فرا گیرید و سپس مشتق.
آرزوی موفقیت برای شما
استاد فرق مشتق با دیفرانسیل در چیست ؟
سلام بر شما
مشتق و دیفرانسیل دو مفهوم مرتبط هستند اما برای درک بهتر تفاوت بین این دو باید مفهوم عملکردها را به خوبی بشناسید.
عملکردها در ریاضی، رابطه بین ورودی ها و خروجی های ممکن هستند. در بحث عملکردها هر ورودی با یک خروجی مرتبط است و مفاهیم متغیر مستقل و متغیر وابسته از جمله مفاهیم مهم این مبحث است.
بعد از فراگیری و شناخت این متغیرها وارد دنیای حساب می شویم که در اساس با ریاضیات متفاوت است و ابزار تعریف مشتق تابع است و علاوه بر محاسبات و جبر، تغییر و حرکت را به ریاضیات کشانده و به آن می پردازد و شامل دو زیر مجموعه حساب دیفرانسیل و حساب انتگرال است.
حساب دیفرانسیل، تغییرات واقعی یک عملکرد را مورد بررسی می گذارد.
مشتق، میزان تغییر یک متغیر با توجه به تغییر متغیر های دیگر را نشان می دهد.
معادلات دیفرانسیل، روابط بین متغیرهای مذکور و مشتقات است.
در پیرامون، مثالهای متنوعی در مورد مشتق و دیفرانسیل وجود دارد.
آرزوی موفقیت
سلام خسته نباشید
من دوست دارم بدونم مشتق در زندگی و یا شغل چه کاربردی دارد؟
لطفا فکر نکنید قصد توهین کردن به ریاضی رو دارم خیلی ممنون میشم جواب بدهید.
سلام بر شما
متشکرم
ببینید ریاضی تاثیرش در زندگی به دید ظاهر شاید ناچیز باشد اما اگر کمی به اطرافتون دقت کنید متوجه تاثیرات آن خواهید شد. به عنوان مثال؛
فرض کن یک مهندس راه سازی میخواد پلی مثلا دارای شیب رو در محلی احداث کنه برای بدست آوردن شیب این پل قانون مشتق به چالش کشیده میشه.
به عنوان مثالی دیگر، فرض کنید جسمی از ارتفاعی به پایین پرت می شود( سقوط آزاد جسم) گالیله مسافتی که جسم طی میکند رو طبق فرمول
x=۱/۲gt^۲
بدست آورد.
حالا اگر بخواین بدونید جسم با چه سرعتی و یا شتابی به سمت پایین حرکت میکند باز هم قوانین مشتق رو باید درگیر کرد.
مثال دوم در مورد سقوط آزاد بود شما در مورد حرکت هواپیماها، بالگردها و… هم قوانین مشتق رو خواهید داشت.
در تغییرات یک کمیت نسبت به کمیتی دیگر قوانین مشتق را خواهیم داشت.
کاربردهای ریاضیات در زندگی
طیف بسیار گسترده ای را شامل می شود.
با عرض سلام و خسته نباشید
چه وقتهایی به جای محاسبه سگما از تابع مشتق گرفته و به جواب می رسیم ؟
ممنون اگر جواب بدید
سلام استاد عزیز فرق مشتق با دیفرانسیل چیست وداستان بیهنایت کوچک ها در ریاضی چه ربطی به مشتق ودیفرانسیل دارد؟
استاد من عاشق ریاضیات هستم فوق لیسانس مهندسی دارم در واقع بدون ریاضی و بالاخص بحث دیفرانسیل گیری مهندسی معنی ندارد خواستم اگه میشه فرق مشتق با دیفرانسیل برام توضیح بدین
استاد عزیز این ایمیل من هستش اگه زحمت نمیشه خواستم با شما در ارتباط باشم چون سوالهای زیادی دارم اگه کمکم کنید لطف بزرگی در حق من کردین
سلام ببخشید شما فیلم نمیزارین؟
سلام
فعلا تدریس آنلاین در برنامه ام نیست. خیلی سرم شلوغه فرصت پیدا نکردم.
سلام خسته نباشی من سال آخرم امسال کنکور دارم ولی اصلا حسابان یا هندسه تو مخم نمیره هر چقدر به کتاب نگاه میکنم بدتر ناامید میشم نمیدونم چیکار کنم ولی درسای دیگه برای من خیلی راحت باید چیکار کنم از نظر شما باید از چه زاویه ای به این درس نگاه کنم؟؟؟؟
سلام بر شما
آرزوی موفقیت برای شما.
مطالعه این دروس هم مانند بقیه دروس است.
اما طبیعی است که به دلیل عدم علاقه درونی خواندن این کُتُب برایتان سخت باشد.
لذا با توجه به اینکه کنکوری هستین و زمان زیادی تا کنکورتان باقی نیست اینکه در این مدت محدود بخواهید شیوه مطالعه تان در این دروس را تغییر دهید نه اینکه نشدنی باشد اما اغلب چندان کارساز نیست.
توصیه من اینست که مطالعه تان در این دروس را به صورت مبحثی پیش ببرید.
مباحثی که در آن توانمندی دارید و نیز در کنکور های گذشته از آن سوال آورده شده است را مطالعه و بسیار در این مباحث تست کار کنید.
حذف این دروس جهت عدم مطالعه برای کنکور و مانور بر روی دروس دیگر که توانمندترین پیشنهاد خوبی نیست.
استاد مطالب رو خیلی ساده و خوب توضیح دادید ممنونم 🙂
میشه لطفا یه توضیحی هم درباره ی مشتق جزئی بزارید.
سلام بر شما
خواهش میکنم تشکر
در رابطه با مشتق جزئی باید بدانید که در ابتدا و در بحث مشتقات، یک تابع بر حسب یک متغیر مستقل تعریف میشد و مشتق یک تابع را نسبت به یک متغیر مستقل بدست می آوردیم.
اما اگر تابع بر حسب چند متغیر تعریف شده باشد و بخواهیم مشتق را نسبت به هر کدام از متغیر ها بدست آوریم مشتق جزئی را بکار میبریم.
در این راستا، باید یک متغیر یا چند متغیر را ثابت در نظر بگیریم تا بتوانیم مشتق جزئی را نسبت به متغیر خواسته شده محاسبه کنیم.
توصیه من این است که برای یادگیری جامع کتاب مطالعه کنید. از جمله، سیلورمن، توماس و…
سلام.خسته نباشید .یه سوال داشتم.
این که مشتق اول یک تابع پیوسته باشه و مشتق دوم تابع ناپیوسته یعنی چی؟
منظور از پیوسته و ناپیوسته بودن مشتق یعنی چی؟
سلام بر شما کاربر گرامی
در واقع سوال اولتون نمیتونه درست باشه چرا که دلیلی ندارد مشتق اول پیوسته و مشتق دوم ناپیوسته باشد.
و اینکه مشتق اول پیوسته و مشتق دوم ناپیوسته میتواند بخشی از قضیه یا … بوده باشد.
و اما مفهوم پیوستگی توابع به طور کلی اینه که نمودار تابع در دامنه خود، بریدگی نداشته باشد.
برای فراگیری دقیق این مبحث، می توانید از کتاب های درسی دبیرستان، کمک درسی یا کتاب های دانشگاهی کمک بگیرید.
از جمله سیلورمن، توماس
تشکر استاد محترم از معلومات خوب تان جهان سپاس……
متشکرم جناب حکمتی
با امید پیشبرد بهتر و گسترده تر این مسیر و رضایتمندی بیشتر شما همراهان
سلام. سوالماین بود که وقتی برای تعیین مقدار مشتق تابعی در یک نقطه از تعریف معادله مشتق استفاده میکنیم مقداری که محاسبه میشه با همون مقدار که از تابع مشتق اون تابع به دست میاد متفاوته دلیلش تقریبی بودنه مقدار مشتق هستش ؟ تابع هم درجه ۲ مثلا y=x2.?
سلام آقای شعبان زاده
مقدار مشتق در یک نقطه چه از طریق تعریف مشتق محاسبه بشه و چه از طریق فرمولات مشتق جواب یکسانی بدست میده. و مقدار مشتق در یک نقطه با استفاده از تعریف مشتق(صرف وجود حد) یک مقدار تقریبی نیست.
در تعریف مشتق اگر مقدار حد متناهی باشه نشان دهنده مشتق پذیر بودن تابع در نقطه مورد نظر است.
سلام استاد، من ترم آخر کارشناسی ریاضی هستم من درس پروژه کارشناسی را انتخاب کردم استاد عنوان آن رادستگاههای تعادل خواه و کاربرد آن در زندگی اجتماعی تعیین کرده لطفا برای جمع آوری مطالب کمکم کنید خیلی ممنون.
سلام
ارتباطی بین دستگاه تعادل سنج(Balance meter) یا دستگاه تعادل(Equilibrium system) و ریاضی پیدا نمی کنم به نظرم این موضوع به فیزیک و آمار ارتباط بهتری پیدا می کند.
اگر اطلاعات بیشتری در مورد موضوع دارید و فکر می کنید با ریاضی ارتباط دارد با ایمیل که در قسمت ارتباط با ما است ذکر کنید در صورتی که ملموس و قابل درک باشد از کمک به شما دریغ نمی کنم.
وای که چقد من از ریاضی میترسم و حس خوبی بهم نمیده مشتق، انتگرال، روووووووووووووووووویه و …
خوشبحالتون استاد.
سلام بر خانم رحمانی فر
ترس شما، اول به این علت است که از ابتدا بخوبی با این درس آشنا و روبرو نشده اید، دوم عدم علاقه است.
از طرفی اگر از این درس ترس نداشتین باز هم، به نقل از زنده یاد پرفسور مریم میرزاخانی خطاب به همه علاقه مندان به این درس:
“ریاضیات زیبایی خود را تنها به شاگردان صبور نشان می دهد”
براتون آرزوی موفقیت در حرفه مورد علاقتون دارم.
خسته نباشید استاد
ممنونم بخاطر زحمت امروز. بسیار عالی بود.
آرزوی موفقیت براتون دارم
سلام متشکرم آقای لهراسبی
سلام
لطفا در مورد روش های مشتق گیری هم توضیح بدید.
موفق باشید.
سلام
بله حتما. ممنونم از توجهتون.
ممنون از معلومات تان
خواهش میکنم. با این امید و تلاش که روز به روز پیشرفت کنیم و آن را به دیگران ارائه دهیم.
سلام
میتونید برام مفهوم هندسی مشتق رو به درستی توضیح بدید لطفا
سلام بر شما کاربر گرامی
مفهوم هندسی مشتق را هم در مقاله و هم در کامنت ها توضیح داده ام لطفا مطالعه شود اگر سوالی بود مجددا بفرمائید.