مثلثات و روابط بین نسبت های مثلثاتی

مثلثات (Trigonometry) علمی است که روابط بین طول اضلاع و زاویه های یک مثلث را بررسی می کند. در این مقاله ، ابتدا مفاهیم مهم و پایه ای توابع سینوس (sin)، کسینوس (cos) و تانژانت (tan) را تعریف خواهیم نمود.
توابع اصلی مثلثات
از آنجایی که مجموع زوایای داخلی هر مثلث 180 درجه است پس، در یک مثلث قائم الزاویه اگر یکی از زوایای تند در دسترس باشد زاویه تند دیگر قابل محاسبه است.
اگر زاویه ها را داشته باشیم می توانیم نسبت بین اضلاع را بدست آوریم. با داشتن اندازه یک ضلع اندازه دو ضلع دیگر بدست می آید. نسبت بین اضلاع با استفاده از توابع اصلی مثلثاتی بدست می آید. برای زاویه تند \(\theta \) داریم:
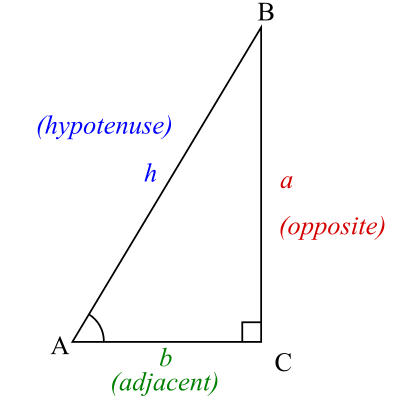
1- تابع سینوس را به صورت نسبت ضلع مقابل به وتر تعریف می کنیم:
2- تابع کسینوس را به صورت نسبت ضلع مجاور به وتر تعریف می کنیم:
3 تابع تانژانت را به صورت نسبت ضلع مقابل به ضلع مجاور تعریف می کنیم:
اتحادهای مثلثاتی
روابط مثلثاتی که برای تمام زاویه ها برقرار هستند اتحاد مثلثاتی نامیده می شوند. کاربرد اتحادهای مثلثاتی در محاسبه مجموع و تفاضل دو زاویه، تعیین مشخصات مثلث، محاسبه تابع های مثلثاتی و… است.
روابط بین نسبت های مثلثاتی
رابطه بین نسبت های مثلثاتی به این صورت است که ما با داشتن هر یک از نسبت های مثلثاتی می توانیم سایر آن ها را بدست آوریم و یا در اثبات اتحادها از آن ها استفاده کرد. همه رابطه هایی که در حد کتاب ریاضی دهم مربوط به مثلثات می شود در زیر آمده است.

\begin{array}{l}
{\sin ^2}\theta = 1 – {\cos ^2}\theta \\
{\cos ^2}\theta = 1 – {\sin ^2}\theta \\
{\cos ^2}\theta = \frac{1}{{1 + {{\tan }^2}\theta }}\\
{\sin ^2}\theta = \frac{1}{{1 + {{\cot }^2}\theta }}\\
\cot \theta = \frac{1}{{\tan \theta }}
\end{array}
\end{array}\)
به کمک این روابط می توان هر نسبت مثلثاتی را به دیگری تبدیل کرد. درمبحث نسبت های مثلثاتی باید به اینکه انتهای کمان در کام ربع ثلثاتی قراردارد بسیار دقت نمود چرا که علامت نسبت مثلثاتی بر این اساس مشخص می گردد.
به عنوان مثال: اگر انتهای کمان زاویه در ربع چهارم قرار داشته باشد علامت سینوس مثبت و علامت کسینوس و تانژانت و کتانژانت منفی می باشد.
\(\begin{array}{*{20}{l}}\begin{array}{l}
{\cos ^2}\theta = 1 – {\sin ^2}\theta = 1 – {(0.8)^2} = 1 – 0.64 = 0.36\\
{\sin ^2}\theta = 1 – {\cos ^2}\theta = 1 – 0.36 = 0.64\\
\to \cos \theta = 0.6,\sin \theta = – 0.8\\
\tan \theta = \frac{{\sin \theta }}{{\cos \theta }} = \frac{{ – 0.8}}{{0.6}} = \frac{{ – 4}}{3}\\
\cot \theta = \frac{1}{{\tan \theta }} = \frac{{ – 3}}{4}
\end{array}
\end{array}\)
مثال: اگر سینوس زاویه ای 0.8 باشد و انتهای کمان زاویه در ربع سوم قرار داشته باشد سایر نسبت های مثلثاتی برای این زاویه را بدست آورید.
اتحاد اصلی(اتحاد فیثاغورث)
اتحادهای فیثاغورثی به صورت زیر می باشند:
\begin{array}{l}
{\sin ^2}A + {\cos ^2}B = 1\\
\sin A = \cos B = \cos (\frac{\pi }{2} – A)\\
\cos A = \sin B = \sin (\frac{\pi }{2} – A)\\
\tan A = \cot B = \cot (\frac{\pi }{2} – A)\\
\cot A = \tan B = \tan (\frac{\pi }{2} – A)
\end{array}
\end{array}\)
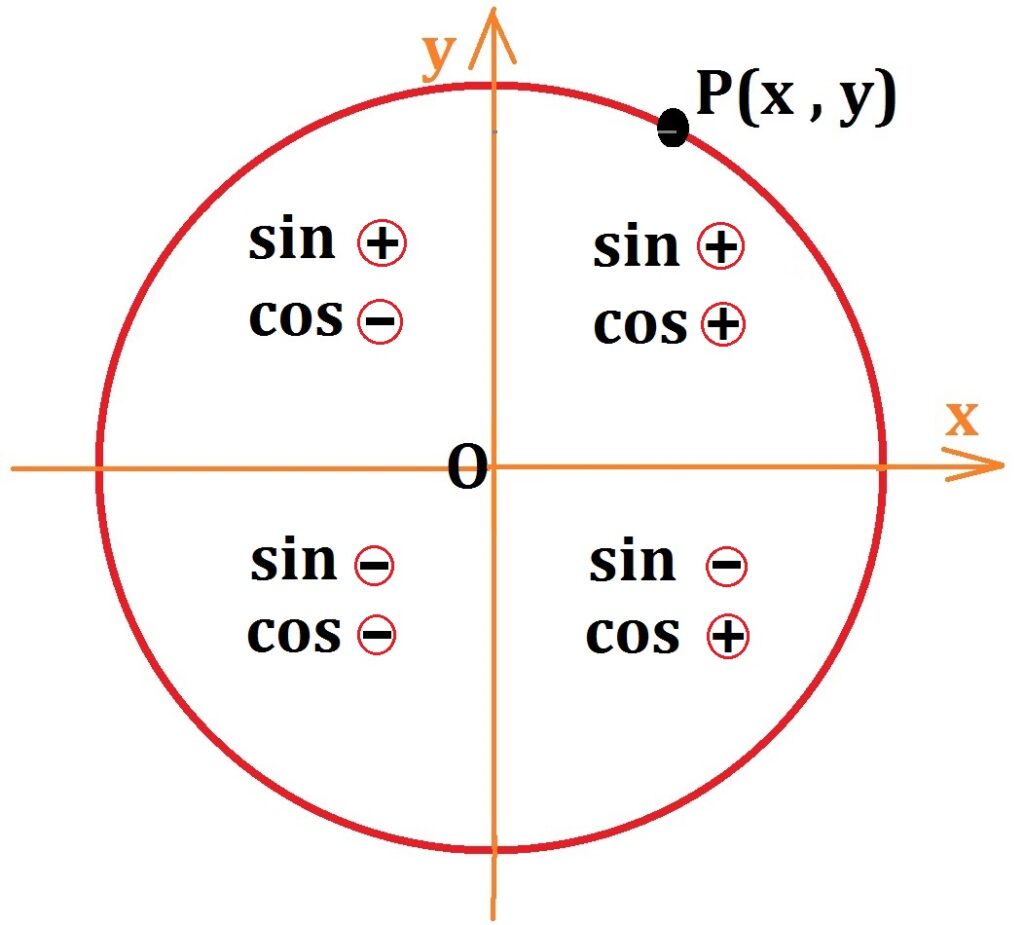
دایره مثلثاتی(Trigonometric circle)
دایره مثلثاتی دایره ای است به شعاع یک که جهت چرخش آن پاد ساعت گرد است و می توان با استفاده از آن نسبت های مثلثاتی و نیز طول ها و زوایا در اشکال هندسی مختلف را بدست آورد.

هر نقطه مثل \(p \) زویاین دایره دارای طول و عرض \(x\) و \(y \) است. اندازه \(y\) مقدار سینوس و اندازه \(x \) مقدار کسینوس را مشخص می کند.
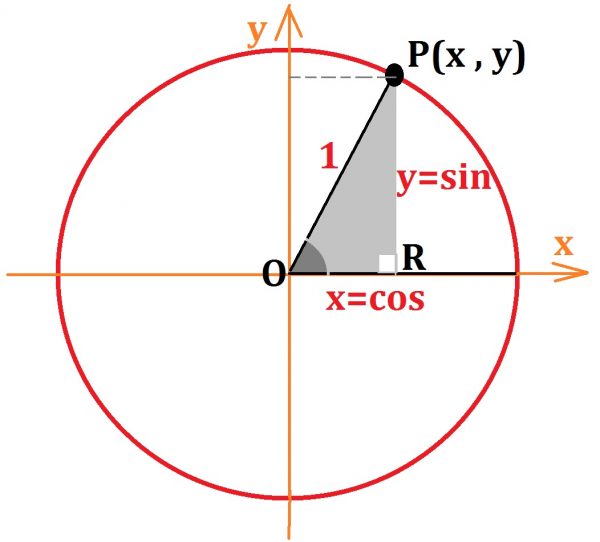
به مثلث OPR در دایره مثلثاتی بالا دقت کنید :
- زاویه O، که در پایین مثلث ایجاد شده است زاویه بین OP و جهت مثبت محور x هاست.
- اندازه PR (ضلع مقابل) برابر است با عرض y نقطه p
- اندازه OR (ضلع مجاور) برابر است با طول x نقطه p
- اندازه وتر مثلث هم یک واحد است.
با استفاده از تعریف سینوس و کسینوس به رابطه های y=sin و x=cos می رسیم. از طرفی مقدارx و y نقطه هایی که روی دایره مثلثاتی قرار می گیرند نمی توانند از 1+ و 1- فراتر روند بنابراین داریم:
از آنجاییکه رابطه فیثاغورث برای هر مثلث قائم الزاویه ای برقرار است بنابراین در مثلث OPR نیز این رابطه برقرار است و رابطه اصلی مثلثات را خواهیم داشت:
\({\sin ^2}\theta + {\cos ^2}\theta = 1\)در دایره مثلثاتی نقطه p می تواند در هر جایی از محیط دایره قرار گیرد و از آنجاییکه نقطه p نوک کمان حرکت در خلاف عقربه ساعت است و در هر جایی از دایره که قرار گیرد نسبت های مثلثاتی دارای علامت مربوط به آن نقطه خواهد بود لذا، دایره مثلثاتی را به چهار ربع تقسیم کرده اند که در بخش های بعدی به آن پرداخته شده است.
برای اینکه راحت تر روند حرکت روی دایره مثلثاتی را ارزیابی کنیم یک دستگاه مختصات دکارتی که مبدا مختصات مرکز دایره باشد درون دایره رسم می کنیم.
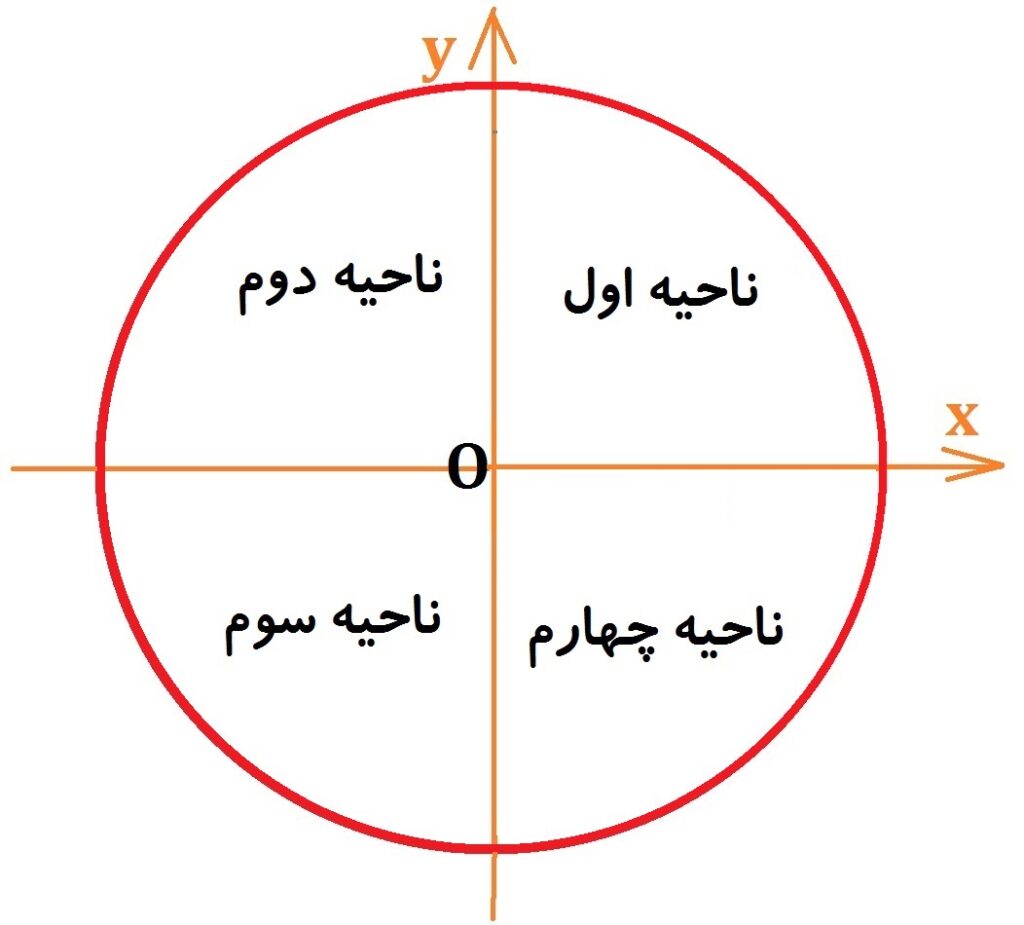
اندازه زاویه در هرناحیه، محدوده خاص خود را دارد که به صورت زیر است:
- زاویه ای که در ناحیه اول قرار می گیرد: بین 0 تا 90 درجه
- زاویه ای که در ناحیه دوم قرار می گیرد: بین 90 تا 180 درجه
- زوایه که در ربع سوم قرار می گیرد: بین 180 تا 270 درجه
- زاویه ای که در ربع چهارم قرار می گیرد: بین 270 تا 360 درجه
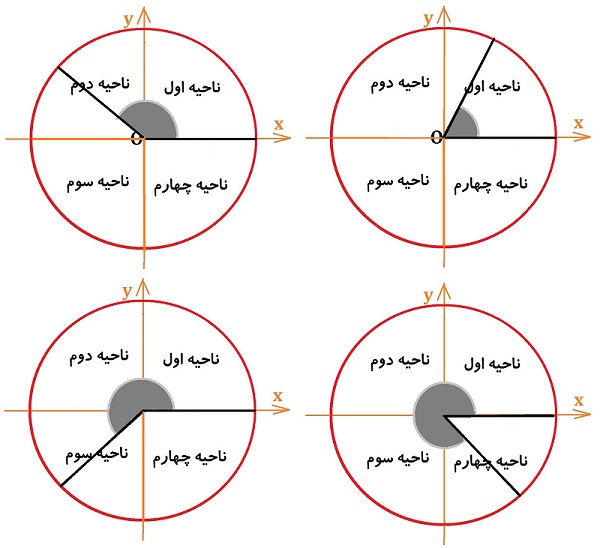
در دایره مثلثاتی و با آگاهی از علامت جهات مختلف محورهای مختصات دکارتی و نیز مطالب فوق، می توان علامت نسبت های مثلثاتی در هر ربع را به صورت زیر نوشت:
- در ناحیه اول: تمام نسبت های مثلثاتی مثبت
- در ناحیه دوم: سینوس مثبت، کسینوس منفی، تانژانت و کتنانژانت منفی
- در ناحیه سوم: سینوس و کسینوس منفی، تانژانت و کتانژانت مثبت
- در ناحیه چهارم: سینوس منفی، کسینوس مثبت، تانژانت و کتانژانت منفی
یکای اندازه گیری
یکاهای اندازه گیری زاویه به 4 دسته زیر تقسیم بندی می شود.
- درجه: یکایی است که از زمانهای گذشته مورد استفاده بوده است. مقدار این یکا با تقسیم بندی دایره به ۳۶۰ قسمت مساوی به دست میآید. به بیان دیگر، یک درجه برابر با زاویه ی روبرو به کمانی است که اندازه ی آن، ۱/۳۶۰ محیط دایره باشد.
- رادیان: یکایی که در محاسبات مربوط به بحث مثلثات مورد استفاده قرار می گیرد. یک رادیان برابر با زاویه ی روبرو به کمانی است که طول آن برابر با طول شعاع دایره متناظر باشد. طبق این تعریف، یک دایره ی کامل برابر ۲π رادیان است. در محاسبات ریاضی که شامل توابع مثلثاتی هستند (مانند معادلات دیفرانسیل و انتگرال)، از یکای رادیان استفاده میشود.
- گرادیان: یک دایره ی کامل ۴۰۰ گراد می باشد. به بیان دیگر، گراد یک صدم ربع دایره است. کاربرد اصلی گراد در محاسبات مربوط به نقشه برداری است.
- دور: یک دور معادل یک دایره ی کامل و برابر با ۳۶۰ درجه یا ۲π رادیان است.
تبدیل واحد(یکا) اندازه گیری به یکدیگربه صورت زیر می باشد:
\(\frac{\pi }{{360}} = \frac{R}{{2\pi }} = \frac{G}{{400}}\)
مقادیر نسبت های مثلثاتی برخی زوایای تند
با رسم یک دستگاه مختصات دکارتی در دایره مثلثاتی و با آگاهی از اینکه محور\(Y\) ها نمایانگر مقادیر سینوس ها و محور\(X\) ها نمایانگر مقادیر کسینوس هاست و نیز با دانشی از ویژگی های مثلث متساوی الساقین، متساوی الاضلاع و رابطه فیثاوغورث در مورد مثلث قائم الزوایه می توانید به سادگی نسبت های مثلثاتی برای برخی زوایای خاص را محاسبه کنید.
\(\begin{array}{*{20}{l}}\begin{array}{l}
\sin 0 = \cos 90 = 0\\
\cos 0 = \sin 90 = 1
\end{array}
\end{array}\)
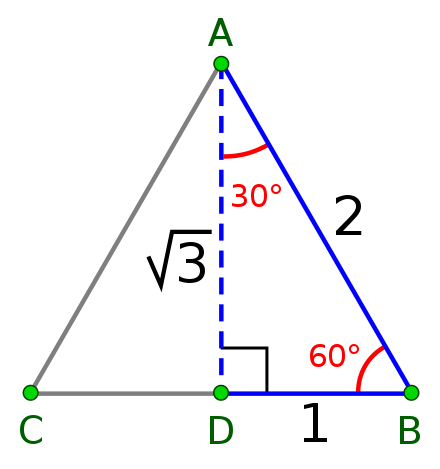
مثلث قائمالزاویهای که یک زاویه ی °۴۵ داشته باشد، زاویه ی تند دیگر آن نیز °۴۵ است و مثلث قائمالزاویه ی متساویالساقین نامیده میشود. در این مثلث، بر پایه قضیه ی فیثاغورس اندازه وتر، ۲√ برابر اندازه ی هر یک از دو ساق است؛ بنابراین:
\(\begin{array}{*{20}{l}}\begin{array}{l}
\sin 45 = \cos 45 = \frac{{\sqrt 2 }}{2}\\
\tan 45 = \cot 45 = 1
\end{array}
\end{array}\)
با استفاده از ویژگی مثلث متساوی الاضلاع و نیز رابطه فیثاغورث می توان به نسبت های زیر رسید:
\(\begin{array}{*{20}{l}}\begin{array}{l}
\sin 30 = \cos 60 = \frac{1}{2}\\
\cos 30 = \sin 60 = \frac{{\sqrt 3 }}{2}
\end{array}
\end{array}\)
در دایره ی واحد، امکان محاسبه ی توابع مثلثاتی برای زاویههای بزرگتر از ۹۰ درجه نیز وجود دارد. مقدار توابع مثلثاتی برای هر زاویهای، مانند شکل زیر تعیین می شود وعلامت یک تابع بر پایه ی مقدار زاویه در دایره ی واحد به صورت آمده در زیر است.
تعیین علامت توابع مثلثاتی
| تابع | ربع اول | ربع دوم | ربع سوم | ربع چهارم |
| سینوس کسکانت | + | + | – | – |
| کسینوس سکانت | + | – | – | + |
| تانژانت کتانژانت | + | – | + | + |
دوران
توابع مثلثاتی برای زاویههای بزرگتر از °۹۰ را میتوان با استفاده از روابط دوران پیرامون مرکز دایره به دست آورد. همچنین زاویههای کوچکتر از صفر با دوران پیرامون محور افقی قابل محاسبه هستند. جدول زیر، نشاندهنده این رابطهها است:
در تلفن همراه، جدول را به سمت راست بکشید.
| دوران حول محور افق | دوران با زاویه ی \(\frac{\pi }{2}\) | دوران با زاویه ی \(\pi \) | دوران با زاویه ی \(2\pi \) |
|---|---|---|---|
| \(\sin ( – \theta ) = – \sin \theta \) | \(\sin (\theta + \frac{\pi }{2}) = + \cos \theta \) | \(\sin (\theta + \pi ) = -\sin \theta \) | \(\sin (\theta + 2\pi ) = + \sin \theta \) |
| \(\cos ( – \theta ) = + \cos \theta \) | \(\cos (\theta + \frac{\pi }{2}) = – \sin \theta \) | \(\cos (\theta + \pi ) = – \cos \theta \) | \(\cos (\theta + 2\pi ) = + \cos\theta \) |
| \(\tan ( – \theta ) = – \tan \theta \) | \(\tan (\theta + \frac{\pi }{2}) = – \cot \theta \) | \(\tan (\theta + \pi ) = + \tan \theta \) | \(\tan (\theta + 2\pi ) = + \tan\theta \) |
| \(\cot ( – \theta ) = – \tan \theta \) | \(\cot (\theta + \frac{\pi }{2}) = – \tan \theta \) | \(\cot (\theta + \pi ) = + \cot\theta \) | \(\cot (\theta + 2\pi ) = + \cot \theta \) |
| \(\sec ( – \theta ) = + \tan \theta \) | \(\sec (\theta + \frac{\pi }{2}) = – \csc \theta \) | \(\sec(\theta + \pi ) = -\sec \theta \) | \(\sec(\theta + 2\pi ) = + \sec \theta \) |
| \(\csc ( – \theta ) = – \tan \theta \) | \(\csc (\theta + \frac{\pi }{2}) = + \sec \theta \) | \(\csc (\theta + \pi ) = -\csc \theta \) | \(\csc (\theta + 2\pi ) = + \csc\theta \) |
ویژگی های توابع مثلثاتی
زوج و فرد بودن
بر اساس تعریف توابع مثلثاتی و نیز دایره ی واحد، میتوان زوج یا فرد بودن هر تابع مثلثاتی را تعیین نمود. بهطور خلاصه:
- کسینوس و سکانت، تابع زوج هستند.( برای مثال: \(\cos ( – \theta ) = \cos \theta \))
- سینوس، تانژانت، کتانژانت و کسکانت، تابع فرد هستند. ( برای مثال: \(\sin ( – \theta ) = -\sin \theta \) )
پیوستگی
توابع سینوس و کسینوس همواره پیوسته و مشتقپذیر هستنند که به راحتی قابل اثبات است. در مورد دیگر توابع مثلثاتی که در مخرجشان یکی از دو تابع سینوس یا کسینوس قرار دارد، همواره پیوسته نیستند. زیرا مقدار توابع سینوس و کسینوس در برخی نقاط برابر صفر است. نقاط ناپیوستگی توابع مثلثاتی به صورت زیر هستند (k یک عدد صحیح دلخواه است):
- تانژانت و کسکانت: \(k\pi \)
- کتانژانت و کسکانت: \(k\pi + \frac{\pi }{2}\)
تناوب
توابع مثلثاتی با یک تناوب مشخص، تکرار میشوند. این تناوب برای توابع تانژانت و کتانژانت، °۱۸۰ و برای سایر توابع مثلثاتی، °۳۶۰ است. برای مثال، تناوب توابع سینوس و تانژانت به صورت رابطه ی زیر است:
\(\begin{array}{*{20}{l}}\begin{array}{l}
\sin \left( {2\pi + \theta } \right) = \sin \theta \\
\tan \left( {\pi + \theta } \right) = \tan \theta
\end{array}
\end{array}\)
مشتق و انتگرال توابع مثلثاتی
مشتق دو تابع مثلثاتی اصلی (سینوس و کسینوس) با استفاده از تعریف مشتق، به دست میآید. برای مشتقگیری سایر توابع مثلثاتی میتوان از قاعده ی مشتقگیری تابع کسری استفاده کرد.
در تلفن همراه، جدول را به سمت راست بکشید.
| تابع مثلثاتی | مشتق اول | مشتق دوم | انتگرال |
|---|---|---|---|
| \(\sin \left( x \right)\) | \(\cos \left( x \right)\) | \(-\sin \left( x \right)\) | \(-\cos \left( x \right)\) |
| \(\cos \left( x \right)\) | \(-\sin \left( x \right)\) | \(-\cos \left( x \right)\) | \(\sin \left( x \right)\) |
| \(\tan \left( x \right)\) | \({\sec ^2}\left( x \right)\) | \(2{\sec ^2}\left( x \right)\tan \left( x \right)\) | \( – \ln \left| {\cos \left( x \right)} \right|\) |
| \(\cot \left( x \right)\) | \({-\csc ^2}\left( x \right)\) | \(2{\csc ^2}\left( x \right)\cot \left( x \right)\) | \( \ln \left| {\sin \left( x \right)} \right|\) |
| \(\sec \left( x \right)\) | \(\sec \left( x \right)\tan \left( x \right)\) | \(\sec \left( x \right)\left( {{{\sec }^2}\left( x \right) + {{\tan }^2}\left( x \right)} \right)\) | \(\ln \left| {\sec \left( x \right) + \tan \left( x \right)} \right|\) |
| \(\csc \left( x \right)\) | \(-\csc \left( x \right)\cot \left( x \right)\) | \(\csc \left( x \right)\left( {{{\csc }^2}\left( x \right) + {{\cot }^2}\left( x \right)} \right)\) | \(-\ln \left| {\csc \left( x \right) + \cot \left( x \right)} \right|\) |
محاسبه ی مقدار توابع مثلثاتی به صورت دستی، پیچیدهاست؛ اما امروزه به دلیل در دسترس بودن رایانهها و ماشین حسابهای مهندسی، که مقدار مورد نیاز را برای هر زاویهای به سادگی به دست میآورند، پیچیدگی آن از بین رفته است.
سه روش متداول برای محاسبه ی مقدار توابع مثلثاتی مورد استفاده است که عبارتند از بهرهگیری از مقدارهای دقیق، روش سنتی جدولهای مثلثاتی و روش نوین بهرهگیری از رایانه.
تابع معکوس مثلثاتی
توابع معکوس مثلثاتی به عنوان قرینه ی توابع مثلثاتی نسبت به خط y=x تعریف میشوند. این تابعها را با افزودن ARC به ابتدای نام تابع اصلی، معرفی میکنند. این تابعها یک عدد حقیقی را میگیرند و یک زاویه را برمیگردانند. توابع مثلثاتی در همه ی دامنه ی خود، یکبهیک و معکوسپذیر نیستند.
برای آن که بتوان تابع معکوس برای این توابع تعریف نمود، باید تابع به دامنهای که در آن معکوسپذیر است، محدود شود. این دامنه، برای توابع مختلف به صورت جدول زیر است.
علاوه بر این، مشتق توابع معکوس مثلثاتی که با روش مشتقگیری ضمنی به دست میآید، در جدول آورده شدهاست.
در تلفن همراه، جدول را به سمت راست بکشید.
| تابع اصلی | دامنه تابع اصلی | تابع معکوس | دامنه تابع معکوس | مشتق تابع معکوس |
|---|---|---|---|---|
| \(y = \sin x\) | \(– \frac{\pi }{2} \le x \le \frac{\pi }{2}\) | \(x = \arcsin y\) | \(– 1 \le y \le 1\) | \(\frac{1}{{\sqrt {1 – {x^2}} }}\) |
| \(y = \cos x\) | \(0 \le x \le \pi \) | \(x = \arccos y\) | \(– 1 \le y \le 1\) | \(-\frac{1}{{\sqrt {1 – {x^2}} }}\) |
| \(y = \tan x\) | \(– \frac{\pi }{2} \le x \le \frac{\pi }{2}\) | \(x = \arctan y\) | اعداد حقیقی | \(\frac{1}{{1 + {y^2}}}\) |
| \(y = \cot x\) | \(0 \le x \le \pi \) | \(x = {\mathop{\rm arccot}\nolimits} y\) | \(\begin{array}{l} 1 \le y\ y \le – 1 \end{array}\) | \(-\frac{1}{{{y^2}\sqrt {1 – {y^{ – 2}}} }}\) |
| \(y = \sec x\) | \(\begin{array}{l} 0 \le x \le \pi \ x \ne \frac{\pi }{2} \end{array}\) | \(x = {\mathop{\rm arcsec}\nolimits} y\) | \(\begin{array}{l} 1 \le y\ y \le – 1 \end{array}\) | \(\frac{1}{{{y^2}\sqrt {1 – {y^{ – 2}}} }}\) |
| \(y = \csc x\) | \(\begin{array}{l} \frac{\pi }{2} \le x \le \frac{\pi }{2}\ x \ne 0 \end{array}\) | \(x = {\mathop{\rm arccsc}\nolimits} y\) | اعداد حقیقی | \(-\frac{1}{{1 + {y^2}}}\) |
کاربرد توابع مثلثاتی
مثلثات کاربرد های زیادی در علوم مختلف از جمله پایه و مهندسی دارد که در زیر چند مورد را ذکر می کنیم.
1- مختصات قطبی، استوانه ای و کروی
2- اعداد مختلط
3- فضای برداری
4- سری فوریه و تبدیل فوریه
5- نقشه برداری
6- فیزیک (نور و مکانیک)
7- برق و مخابرات
8- حرکت های نوسانی
فضای برداری
در ریاضیات و فیزیک، از بردارها برای نشان دادن یک کمیت برداری (که دارای اندازه و جهت است) استفاده میشود. بسیاری از کمیتهای اصلی فیزیک مانند مکان، نیرو و میدان دارای ماهیت برداری هستند.
در برخی محاسبات فضای برداری از توابع مثلثاتی استفاده میشود. برای نمونه، ضرب داخلی دو بردار x و y را میتوان به کمک قانون کسینوسها به صورت زیر محاسبه کرد:
\(\begin{array}{l}x.y = \cos \theta .\left| x \right|.\left| y \right|\
x \times y = \sin \theta .\left| x \right|.\left| y \right|
\end{array}\)
\(\theta \)، زاویه بین دو بردار x , y است.
مختصات قطبی، کروی و استوانه ای
توابع مثلثاتی، پایه ی تعریف دستگاه مختصات قطبی هستند که در ساده سازی بسیاری از مسائل ریاضیات و فیزیک از جمله برخی انتگرالها مؤثر است.
در این دستگاه مختصات، به جای طول و عرض (x,y) یک نقطه (که در دستگاه مختصات دکارتی به کار میرود)، فاصله ی آن با مرکز و زاویه ی بردار گذرنده از مرکز و آن نقطه نسبت به خط افقی (r,θ) به عنوان مختصات یک نقطه در نظر گرفته میشوند.
تبدیل مختصات دکارتی به مختصات قطبی و برعکس با استفاده از توابع مثلثاتی انجام میشود.
\(\begin{array}{l}x = r\cos \theta \\
y = r\sin \theta
\end{array}\)
دستگاههای مختصات استوانهای و کروی که تعمیمیافته ی مختصات قطبی در سه بعد هستند نیز بر مبنای توابع مثلثاتی شکل گرفتهاند. از این دستگاهها در مسائلی مانند انتگرالهای سهبعدی که دارای تقارن استوانهای یا کروی هستند استفاده میشود.
اعداد مختلط
با استفاده از تعریف مختصات قطبی میتوان اعداد مختلط را به صورت توابع مثلثاتی بیان کرد:
\(z = \left| z \right|\left( {os\theta + i\sin \theta } \right)\)که در آن، \(\left| z \right|\) و \(\theta \) زاویه ان با محور افقی و i بردار یکه موهومی است. علاوه برا این، فرومول اویلر که رابطه میان تابع نمایی و تابع مثلثاتی را نشان می دهد به صورت زیر است:
\({e^{i\theta }} = \cos \theta + i\sin \theta \)در اینصورت داریم:
\(\begin{array}{*{20}{l}}\begin{array}{l}
\sin \theta = \frac{{{e^{i\theta }} – {e^{ – i\theta }}}}{{2i}}\\
\cos \theta = \frac{{{e^{i\theta }} + {e^{ – i\theta }}}}{2}
\end{array}
\end{array}\)
می توان سینوس و کسینوس را به ترتیب، جزء مجازی و حقیقی تابع نمایی مختلط در نظر گرفت:
\(\begin{array}{*{20}{l}}\begin{array}{l}
\sin \theta = {\rm{Im}}\left( {{e^{i\theta }}} \right)\\
\cos \theta = {\rm{Re}}\left( {{e^{i\theta }}} \right)
\end{array}
\end{array}\)
فرمول اویلر در شکل توسعه یافته همان فرمول دموآر است که به صورت زیر بیان می شود.
\({e^{in\theta }} = {\left( {\cos \theta + i\sin \theta } \right)^n} = \cos n\theta + i\sin n\theta \)نقشه برداری
مثلثات، پایه ی بیشتر روش های نقشه برداری است. زاویه یابی با دستگاه یا بدون دستگاه، امتداد یابی با روش ژیزمان، سیستم تصویر برای تبدیل تصویر از سطح بیضوی به سطح مستوی، ارتفاع یابی با دستگاه ترازیاب، پیمایش باز و بسته، طراحی قوسها در راهسازی و تبدیلهای دوبعدی در نقشه برداری هوایی، بخشی از کاربردهای توابع مثلثاتی در نقشهبرداری هستند.
برای نمونه، در مثلث سازی که یکی از روشهای قدیمی نقشه برداری است، با استفاده از اندازهگیری زاویه ی یک نقطه نسبت به دو نقطه معین، مختصات آن نقطه را محاسبه میکنند که امروزه از این روش برای اندازهگیری سه بعدی نوری استفاده میشود.
در مثلثسازی از قانون کسینوسها و قانون سینوسها برای محاسبه ی زاویه ی مثلثها و تعیین دقیق موقعیت هر نقطه استفاده میشود.
پیمایش روشی برای نقشه برداری یک محدوده ی باز یا بسته با استفاده از اندازهگیری زاویهها و فاصلهها است. از توابع مثلثاتی برای محاسبه ی موقعیت ایستگاهها استفاده میشود.



57 Comments
سلام و تشکر
سوال من این است که در بسط تیلور تابع سینوس چرا بجای x مقدار زاویه را برحسب رادیان بگذاریم جواب می دهد ولی بازای درجه قرار بدهیم جواب غلط است علت چیست مثلا” زاویه 30 درجه ؟
با تشکر مجدد
سلام مقایسه تانژانت ۱ با تانژانت ۲ و …. در دایره مثلثاتی به چه صورته؟
سلام وقتتون بخیر ان شاء الله که همیشه خوب و سرحال باشید
ببخشید یه سوال داشتم♥️
اگر تتا کوچکتر از ۶۰و بزرگتر از صفر باشد آنگاه ۳ضربدرتتا منهای ۵۰ در کدام ناحیه قرار دارد
سلام بر شما کاربر گرامی
متشکرم
تتا را با دو علامت کوچکتری بین دو عدد صفر و 60 قرار دهید
60>تتا>0 حال، طرفین را در 3 ضرب کرده و منهای 50کنید یعنی؛
130>3تتا منهای 50>0 بنابراین جواب سوال شما میتواند ربع اول یا دوم باشد و بستگی به مقدار تتا دارد.
موفق باشید.
سلام ببخشید میشه این سوال رو جواب بدید
طول قطر های یک چهار ضلعی محدب 12و18 و زاویه بین 2قطر 30 درجه می باشد مساحت این چهار ضلعی چقدر است؟
سلام بر شما کاربر گرامی
برای بدست آوردن مساحت چهارضلعی محدب
حاصلضرب دو قطر را ضربدر زاویه بین کنید و حاصل را تقسیم بر ۲ کنید. موفق باشید
سلام عالی و مفید بود
در فرمول طلایی مثلثات برای کسینوس دو تتا چرا اتحاد مزدوج نمیزنند ممنونم بسیار عالی
سلام بر شما کاربر گرامی
علت اینکه در فرمول طلایی مثلثات مزدوج نمیزنند اینست که دو رابطه تعریف شده یکی بر اساس ( a)sin^۲ و دیگری بر اساس (a)cos^۲ میباشد. مقدار این دو به ترتیب برابر است با ۲/(coa۲a+۱-) و ۲/(coa۲a+۱).
موفق و موید باشید.
سلام وقتتون بخیر باشه…
استاد میشه جواب این سوال رو بدست بیارین؟؟
مساحت یک لوزی به ضلع 8 سانتی متر که یکی از زاویه های داخلی آن 60 درجه میباشد را بدست آورید..
سلام بر شما کاربر محترم
در ابتدا باید بدانید که قطرهای یک لوزی عمود منصف های یکدیگرند و مساحت یک لوزی را میتوان از حاصلضرب قطرهای آن تقسیم بر ۲ بدست آورد. کافیست با رسم نیمساز زاویه و داشتن مقدار ضلع داده شده و با کمک توابع مثلثاتی مقدار نصف یکی از قطرها را محاسبه کنید در ادامه با بکار بستن اتحاد فیثاغورث مقدار نصف دیگر از قطر دیگر را بدست خواهید آورد. هر دو اندازه بدست آمده را در ۲ ضرب کرده تا اندازه قطرها بدست آید سپس با فرمول گفته شده در ابتدای توضیحاتم مساحت را محاسبه نمائید.
موفق باشید.
با سلام
آیا نسبت های مثلثاتی تنها برای مثلث قائم الزاویه قابل تعریف است یا برای هر مثلث دیگری قابل تعریف است؟
سپاس بی کران🙏
سلام بر شما کاربر محترم
نسبت های مثلثاتی برای زوایا تعریف میشوند و زاویه هم تشکیل شده از دو نیم خط که در یک نقطه برخورد دارند.
بنابراین برای هر زاویه در هر مثلثی نسبت های مثلثاتی قابل تعریف است.
موفق باشید
سلام وقت بخیر. چطوری میتونیم از سینوس یا کسینوس یا تانژانت یک زاویه به اندازه ی خود زاویه برسیم؟ خیلی ممنون. واقعا به پاسخ این سوال نیاز دارم. سایتتون عالیه
سلام خسته نباشید.
چطور میتونیم از مقدار های سینوس و کسینوس و تانژانت و کتانژانت مقدار زاویه ی مورد نظر رو بدست بیاریم (البته غیر از زوایای پرکاربرد مثل سی و نود و شصت و چهل و پنج).
اگر چنین راه حلی وجود داره میشه بگین؟
اگر وجود داشت پس سکانت و کسکانت رو هم بگین.
خیلی ممنون.
سایتتون عالیه
سلام بر شما کاربر محترم
اگر بخواهید با داشتن مقدار نسبت های مثلثاتی یک زاویه به اندازه زاویه مورد نظر دست پیدا کنید بایستی از طرفین arc (معکوس)گرفته در اینصورت در یک طرف، arc یک نسبت مثلثاتی با آرگومان(زوایه آن نسبت) برابر میشود و در طرف دیگر بایستی arc مقدار نسبت مثلثاتی را با استفاده از فرمول های مثلثاتی مربوطه یا ماشین حساب های مهندسی بدست آورید.
موفق و سربلند باشید
سلام
ببخشید tan^2 تانژانت به توان ۲ رو چطور میشه تو ماشین حساب محاسبه کرد ممنون
سلام بر شما کاربر محترم
در فرصتی مناسب، نحوه کار کردن با ماشین حساب مهندسی رو سعی کنید در یوتیوب یا آپارات فرا بگیرید.
با این حال، پیشنهاد من اینه که چون توان دوم یک نسبت مثلثاتی رو میتوان به صورت (نسبت مثلثاتی) به توان دو نوشت
لذا شما ابتدا یک پرانتز را باز و بسته کرده و درون آن نسبتِ به عنوان مثال tan a را نوشته و سپس پرانتز را به توان دو برسانید.
موفق باشید.
سلام می بخشید sin به توان 5 تتا چگونه حل میشه. ممنونم
سلام ببخشید sin60کوچک تر از cos30درسته ؟؟
سلام بر شما کاربر محترم
خیر. اشتباست.
این دو فرمول مثلثاتی برابر است.
sin۶۰=cos۳۰= رادیکال ۳ تقسیم بر ۲=۰.۸۵
آرزوی موفقیت برای شما
برای فصل دایره و مثلث و اینا ها چه نرم افزاری برای جواب دادن هست؟
سلام بر شما کاربر گرامی
لطفا منظور سوالتان را واَضح بیان کنید.
نرم افزار برای پاسخ دادن به چه چیزی؟
اگر منظورتان حل تمارین مثلثاتیست هیچ نرم افزاری پاسخگوی
خواسته شما نیست.
موفق باشید.
سلام در رابطه ریاضیات در چرخش خط لوله در پایپینگ میخواهم یاد بگیرم این امر بر پایه مثلثات است
سلام بر شما کاربر گرامی
بله چرخش خط لوله در پایپینگ بر پایه مثلثات و فیثاغورث است.
rolling offsetبه معنای چرخش لوله است. در پایپینگ این اصطلاح بدین معنیست که راستای لوله در هر سه بعد تصویر داشته باشد، یعنی لوله راستایی کاملاً فضایی داشته باشد.
یکی از حالتها اینست که لوله در یکی از جهات اصلی حرکت کرده و سپس در یکی دیگر از جهات اصلی دستخوش چرخش می شود.
فرض کنید میزان حرکت لوله در جهات اصلی را داریم و می خواهیم زاویۀ زانویی را حساب کنیم.
ساده ترین راه که کمترین اشتباه را در پی دارد اینست که از راه فیثاغورث اندازه ی وتر که همان طول لوله و سنتر زانویی های دو سمت لوله است محاسبه شده C^2 = A^2 + B^2 و اندازه ی ضلع مجاور زاویه که همان جابجایی لوله در راستای اصلی است B بر آن تقسیم شود.
مقدار به دست آمده کسینوس زاویه ی چرخش لوله یا همان زاویه ی زانویی است.
cos α = B/C با به دست آمدن این مقدار می توان زانویی 90 یا 45 درجه را بریده و به زانویی مناسب دست یافت.
حالت پیچیده تر چرخش سه بعدی است؛ یعنی لوله ابتدا در یکی از راستاهای اصلی حرکت کرده و سپس طوری می چرخد که در هر سه بعد تصویر داشته باشد.
راه حل چندان پیچیده نیست.
در این حالت هم طول وتر از طریق رابطه ی C^2 = N^2 + E^2 + U^2 به دست می آید که C مشابه بالا نماینده ی اندازه ی وتر است، N میزان حرکت لوله در راستای شمال (جنوب با علامت منفی)، ٍE میزان حرکت لوله در راستای شرق (غرب با علامت منفی) و U مقدار حرکت لوله به سمت بالاست (پایین با علامت منفی).
البته چون مقادیر به توان 2 می رسند، منفی و مثبت اعداد چندان تفاوتی نمی کند.
به دست آمدن زاویه ی زانویی هم مشابه روش اول است یعنی تصویر لوله در راستایی که از قبل حرکت می کرده بر انداز ه ی وتر تقسیم شده و کسینوس زاویه ی زانویی به دست می آید.
برای هر کدام از این حالتها براحتی میتوانید تصویر سازی نمائید.
آرزوی موفقیت برای شما
برای زوایای ربع های دوم، سوم و چهارم با توجه به ربع اول، چگونه می توان نسبت های مثلثاتی را محاسبه نمود?????????
سلام بر شما کاربر گرامی
اولین قدم مهم شناخت و یادگیری دایره مثلثاتی است.
دومین قدم یادگیری علامت زاویه مورد نظر با توجه به قرار گرفتن در ربع مربوطه هست.
سومین قدم دانستن یکسری فرمول های مثلثاتی مربوط به زوایای بزرگتر از ۹۰ درجه و قوانین مربوط به آن است. همچنین فرمول های مثلثاتی مربوط به مجموع و تفاضل زوایا. و…
آرزوی موفقیت برای شما
سلام
مشتق کسینوس رادیکال صفر در نقطه صفر برابر با چه عددی است؟
میشود روش حا را توضیح دهید
سلام و روزتون بخیر
لطفا اگر اشتباه میکنم اصلاح کنید
احساس میکنم تناقضی بین دو شکل (یکی در Trigonometric circle و در تعیین علامت توابع مثلثاتی) وجود دارد. چرا که در شکل اول، کوسینوس در ربع چهارم مثبت علامت گذاری شده است (که فکر میکنم درست باشد) ولی در جدول تعیین علامت توابع مثلثاتی، کوسینوس در ربع چهارم منفی علامت گذاری شده است.
سلام بر شما کاربر محترم
ممنون از شما که من را متوجه خطای انجام شده ساختید.
بله کاملا حق با شماست و اصلاح کردم.
قطعا موفق میشوید.
درود بر شما سرکار خانم فرزامی
کلاس هایی که با شما گرفتم بسیار مفید بوده واسم و یقینا تا آخر هم همینطور خواهد بود.
فقط میتونم بگم بسیار خوشحالم که دارم به ریاضی علاقه مند میشم و میتونم برای کنکور رو خودم حساب وا کنم.
انقد که بیانتون شیوا و مسلط بر موضوع تدریس میکنید و خوش برخورد و با حوصله هستین.
کاش میشد شما واسه دبیرستان پسرانه ما هم تدریس کنید.
امیدوارم هر روز بهتر از قبل بدرخشید برای دانش آموزان و دانشجوهاتون.
سال خیلی خوبی پیش رو داشته باشید همراه با سربلندی و شادی.
سلام بر شما دانش آموز محترم
خداروشکر که کلاس ها مورد رضایتتون قرار گرفته و البته تلاش خودتون مهمتر از تدریس من در طی دوره بود.
متشکرم از حُسن نظرتون نسبت به من. برای شما و سایر دانش آموزان و دانشجویان سربلندی آرزو میکنم و انشالله سال خوبی پیش روی همتون باشه.
سلام وقتتون بخیر
تانژانت در بی نهایت رو هم توضیح بدین.
مثلا تانژانت عدد مشخصی تقسیم بر صفر یا برعکس تانژانت صفر تقسیم بر عدد جوابش چی میشه؟؟
سلام بر شما کاربر محترم
در سوالی که مطرح کردید تانژانت یک عدد بر صفر یا همان تانژانت بینهایت نداریم و تانژانت صفر بر هر عدد یا همان تانژانت صفر، صفر است.
توصیه میکنم دایره مثلثاتی را ترسیم کرده و نسبتهای مثلثاتی برای زاوایای مختلف را بررسی و نسبت های مهم را حفظ کنید.
روابط مثلثاتی را حفظ کنید.
آرزوی موفقیت برای شما.
در بازه صفر تا نود سینوس صعودی و مثبت کسینوس نزولی و مثبت تانژانت مثبت و صعودی اما شیب تانژانت بیشتر از سینوس است تانژانت یعنی سینوس تقسیم بر کسینوس که کسینوس صفر میشود یک و کسینوس نود میشود صفر کسینوس از یک به صفر میل میکند مخرج تانژانت ازیک به صفر میل میکند پس تانژانت درنود بینهایت میشود اما صورت سینوس از صفر به یک میرود پس تانژانت از سینوس شیب بیشتری دارد
بسیار عالی و مفید.سپاسگزارم
سلام بابت این معلومات مفید خیلی ممنون. ببخشید یک استاد داشتیم بهمون می گفت که هرگاه cosیک عددnپای باشه cosعدد همیشه صفر هستش آیا این درسته ؟
پیشه بهم جوابشو بدین .
درود بر شما کاربر محترم
متشکرم
خواهش میکنم اما سوالتون رو دارید اشتباه بیان میکنید.
صورت این سوال با چیزی که شنیدین قطعا متفاوتِ.
ضمنا؛ کسینوس برای یک عدد تعریف نمیشه بلکه برای زاویه یا کمان تعریف میشه در واقع آرگومان توابع مثلثاتی عدد نیست و زاویه است.
هر زمان سوال رو پیدا کردین مجددا مطرح بفرمائید پاسخ خواهم داد.
آرزوی موفقیت برای شما
سلام نمودار سینوس به توان دو را رسم میکنید
سلام بر شما کاربر محترم
در واتساپ سوالتون رو مطرح کنید یا ایمیلی ارسال نمائید تا براتون رسم کرده و ارسال کنم.
شماره تماسم در سایت هست.
سلام سایت و نرمافزار جئوجبرا براتون هر تابع و نموداری رو رسم میکنه میتونید استفاده کنید
سلام
فرق سینوس به توان ۲ سی درجه با سینوس سی درجه به توان ۲ چیه؟
سلام بر شما کاربر محترم
جواب سوال شما اینست که معادلند و این ویژگی در مورد تمام نسبت های مثلثاتی با هر توانی صادق است.
موفق باشید
سلام خود ۱۸۰و۲۷۰و۳۶۰درجه در کدام ربع قرار دارند؟؟؟
سلام بر شما کاربر گرامی
در دایره مثلثاتی زوایایی را که ذکر کردین مشخص نمایید. و از مبدا دایره دستگاه مختصات دکارتی را رسم کنید. با شروع از زاویه صفر و حرکت در خلاف جهت عقربه ساعت میبینیم که در هر ربع دایره ۹۰ درجه طی میشود و زاویای ۹۰، ۱۸۰، ۲۷۰ و ۳۶۰ درجه در راستای محور افق یا عمود قرار دارد.
با توجه به اینکه محور y ها به محور سینوس ها و محور افق به محور کسینوس ها معروف است و همچنین با توجه به اینکه محور افق و عمود دو جهت منفی و مثبت دارد لذا؛ مقدار زاویای مثلثاتی سینوس و کسینوس برای هر کدام از این زاویا را میتوان با عنایت به نکته ذکر شده محاسبه کرد و از اینرو مقدار دیگر مثلثاتی با داشتن سیسنوس و کسینوس قابل محاسبه است.
پس، زوایای گفته شده در هیچ ربعی قرار ندارند.
آرزوی موفقیت برای شما
سلام خسته نباشید
در مورد مقایسه نسبت های مثلثاتی مثلا cos30بزرگتر است یا sin۱۰ چطور باید عمل کرد
سلام بر شما کاربر محترم
ممنونم
شما دایره مثلثاتی رو برای خودتون رو کاغذ ترسیم کنید و مرکز دایره را مبدا دستگاه دکارتی در نظر بگیرید. محور y ها معرف مقادیر sin و محور x ها معرف مقادیر کسینوس می باشد.
از آنجایی که مقادیر sin و cos هر زاویه ای بین حداقل ۱- و حداکثر ۱+ است و نیز بوضوح رو دایره مثلثاتی مشهود است بنابراین با آگاهی از اینکه زاویه میزان چرخش یا کمانی از دایره است که دو نیم خط نسبت به یکدیگر حول مبدا دارند و هم چنین با در نظر گرفتن اینکه علامت توابع مثلثاتی در هر ربع از دایره مثلثاتی چگونه است براحتی میتوان به عنوان مثال فهمید که با دور شدن از زاویه صفر تا حداکثر ۹۰ درجه میزان sin افزایش و مقدار کسینوس کاهش پیدا میکند.
در حالتی که آرگومانها متفاوت است بایستی مقدار تابع را محاسبه کنید. با این حال، اگر بخواهیم مقدار دو تابع مثلثاتی متفاوت با آرگومان متفاوت را قیاس کنیم با توضیح مثال خودتون بدین ترتیب عمل میکنیم( یه جورایی استفاده از رابطه تعدی):
مقدار کسینوس ۳۰ درجه و سینوس ۳۰ درجه را مقایسه میکنیم و سپس مقدار سینوس ۳۰ درجه را با سینوس۱۰ درجه.
موفق باشید.
من میخواستم بدونم که معنی رادیکال چی هستش وقتی میگن رادیکال ۲۵ بعدش میشه ۵ یعنی چه .خب چرا اعداد وزیر رادیکال میبرن.خب از همون اول بگن ۵ .
درود بر شما کاربر محترم
رادیکال یک عدد یعنی ریشه n ام عدد. وقتی ریشه n ام یک عدد را به توان برسونیم میرسیم به عدد مورد نظر.(n بزرگتر مساوی۲)[ریشه دوم یک عدد را جذر عدد و عدد زیر رادیکال در ریشه دوم مجذور است].
مثلا؛ اگر ۵ رو به توان ۳ برسونیم میشه ۱۲۵ پس ۵ میشه ریشه سوم عدد۱۲۵ به عبارتی رادیکال ۱۲۵ با فُرجه ۳ میشه ۵.
و اما چرا از یک عدد ریشه گیری میکنیم؟
ریشه گیری، معکوسِ توان است. وقتی شما یک عدد رو به توان میرسونید آن عدد را با ضرب کردن در خودش، به تعداد توان آن عدد، بزرگ میکنید پس؛ با ریشه گیری از یک عدد آن را کوچک میکنید.
موفق باشید.
مختصر و مفید بود
سلام یک سوال داشتم رابطه زیر مربوط به چه فرمول مثلثاتی میشه؟
C=R sina cosb
متشکرم.
سلام بر شما کاربر محترم
در سوالی که مطرح کردین باید مشخص نمائید C چیست؟!!!!
لطفا سوال خودتون رو دقیق مطرح کنید.
اینکه این رابطه مربوط به چه فرمول مثلثاتی است گنگ است که منظورتان چیست!
در مختصات قطبی، x=rsina و y=rsinb را داریم در روابط مثلثاتی 2sinacosa=sin2a رو داریم و…
باید سوالتان دقیق عنوان بشه تا بتوانم کمکتان کنم.
آرزوی موفقیت
سلام استاد
یک سوال داشتم حجم لوزی که ارتفاع در راس ها هر کدام متفاوت و همچنین ارتفاع مرکز لوزی یک عدد دیگر هست را چگونه به دست می آوریم.
باتشکر
سلام بر شما کاربر محترم
اولا می دانید که لوزی یک شکل هندسی دوبعدی است و زمانی یک شکل هندسی دارای حجم میشود که در فضای سه بعدی قرار گیرد.
با توجه به اینکه در راس های لوزی ارتفاع ایجاد کرده اید بنابراین شکل حاصل یک منشور است که حجم آن از حاصلضرب مساحت قاعده (لوزی) در ارتفاع بدست می آید.
اگر از هر کدام از راس ها به یک اندازه ارتفاع ایجاد کنیم شکل حاصل یک مکعب است.
آرزوی موفقیت برای شما
سلام استاد
تست مثلثات توی کنکور چرا انقد سخت؟
راه حلی وجود داره که بشه راحتتر تست زد؟
سلام بر شما
در بحث مثلثات حفظ فرمول کمک چندانی به شما نمیکند بلکه میبایست با تکرار زیاد فهمید که هر فرمول چگونه به دست آمده است. مطمئن باشید حل تمرینات زیاد در جهت تبدیل معادله های مختاف مثلثاتی به یکدیگر و نیز مسائل مختلف دیگر از مثلثات، شما را در چالش حل تست های مثلثات موفق خواهد کرد.