بررسی جامع دنباله ها و سری ها

در این مقاله، سعی بر آن داریم که مطالب مفید و جامعی از دنباله ها (sequence) و سری ها (Series) در ریاضیات، را بیان کنیم. در ابتدا الگوها را بررسی کرده سپس مفهوم دنباله و انواع دنباله ها را به تفکیک شرح می دهیم و در انتها مقاله را با بررسی مبحث سری ها به پایان می رسانیم.
بسیاری از پدیده های طبیعی در اطراف ما و در زندگی روزمره از الگوهای خاصی پیروی می کنند. نظم ثابتی که در جهان وجود دارد را نیز می توان به کمک الگوهای ریاضی نشان داد. در ریاضیات اعداد از الگوهای بیشمار و جالبی برخوردارند. بسیاری از این الگوها را با نام های مشخصی می شناسیم. دنبالههای حسابی، هندسی، فیبوناچی و اعداد مثلثی نمونه هایی از این الگوها هستند که هر کدام شرایط ویژه ای دارند و از قوانین خاصی پیروی می کنند و در ادامه به تفصیل هر کدام خواهیم پرداخت.
دنبالهها – Sequences
دنباله، تابعی با دامنه اعداد طبیعی (یا زیرمجموعه ای از اعداد طبیعی) و برد آن مجموعه ای نا تهی است. اعدادی که در برد دنباله قرار دارند را جملات دنباله گوییم. این توابع، کاربردهای زیادی در حساب دیفرانسیل و انتگرال و دیگر شاخههای ریاضیات دارد. گاهی، نام دنباله تغییرمیکند به عنوان مثال در نظریه تحلیلی اعداد، به دنبالهها، تابع حسابی میگویند.
جمله عمومی دنباله
برای مشخص کردن یک دنباله، مثل هر تابع دیگری دامنه و ضابطه آن را مشخص میکنیم. در اصطلاح عمومی به ضابطه دنباله، جمله عمومی دنباله گویند. جمله عمومی یک دنباله در واقع قانونی است که از طریق آن هر عضو دامنه به یک عضو از مجموعه برد متناظر میشود یعنی، جمله عمومی به ازای هر مقدار از متغیر\(n\)، جملات دنباله را تولید میکند. جمله عمومی یک دنباله را با نماد \({a_n}\) نمایش می دهیم.
رابطه بازگشتی – دنباله بازگشتی
در بسیاری از دنباله ها بین هر دو جمله متوالی ارتباطی وجود دارد که به وسیله آن می توان جمله بعدی دنباله را تعیین نمود. به چنین رابطه ای، رابطه بازگشتی دنباله مذکور گوییم. دنباله هایی که دارای چنین رابطه هایی هستند را دنباله های بازگشتی مینامند.
حد دنباله
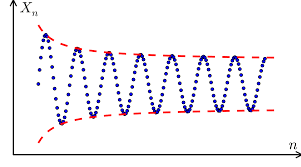
با توجه به اینکه می دانیم دنباله یک تابع است پس، می توان حد تابع دنباله را محاسبه نمود. حد یک دنباله مقداری است که در صورت وجود، جملههای آن دنباله با پیشروی به اندازه دلخواه، به آن نزدیک میشوند.
گوییم دنباله \({a_n}\) دارای حد \(L\) است، هرگاه برای هر عدد \(\varepsilon > 0\)، عددی طبیعی مانند \(M\) وجود داشته باشد به طوری که برای هر عدد طبیعی \(n\) که \(n \ge M\)، نابرابری \(\left| {{a_n} – L} \right| < \varepsilon \) برقرار باشد.
حد دنباله در صورت وجود یکتا میباشد. یعنی، اگر
\(\mathop {\lim }\limits_{n \to \infty } {a_n} = {l_1},\mathop {\lim }\limits_{n \to \infty } {b_n} = {l_2} \Rightarrow {l_1} = {l_2}\)یکی از ویژگیهای حد دنباله به صورت ذکر شده در زیر است.
اگر برای هر \(n\) بزرگتر از \({N_0}\) ( از یک جایی به بعد) داشته باشیم \({a_n} \ge {b_n}\) آنگاه \(\mathop {\lim }\limits_{n \to \infty } {a_n} \ge \mathop {\lim }\limits_{n \to \infty } {b_n}\) .
قضیه فشردگی در دنبالهها
اگر برای هر \(n\) بزرگتر از \({N_0}\) ( از یک جایی به بعد) داشته باشیم \({a_n} \le {c_n} \le {b_n}\) و نیز، \(\mathop {\lim }\limits_{n \to \infty } {a_n} = \mathop {\lim }\limits_{n \to \infty } {b_n} = l\) آنگاه داریم:
\(\mathop {\lim }\limits_{n \to \infty } {c_n} = l\)انواع دنبالهها
در ادامه انواع دنبالهها را مورد بررسی قرار داده و ویژگیها و شرایط هر کدام را ذکر میکنیم.
1- دنباله حقیقی (Real sequence)
دنباله ای که برد آن مجموعه اعداد حقیقی باشد.

2- دنباله متناهی (Finite sequence)
اگر دامنه دنباله زیر مجموعه ای متناهی (قطعه ای) از اعداد طبیعی باشد، دنباله را متناهی گوییم.
3- دنباله نامتناهی (Infinite sequence)
اگر دامنه دنباله مجموعه اعداد طبیعی یا زیر مجموعه ای نامتناهی از اعداد طبیعی باشد، دنباله را نا متناهی گوییم.
4- دنباله کراندار (Boundary sequence)
دنباله \({a_n}\) را کراندار است هر گاه عدد حقیقی و مثبت \(k\) چنان وجود داشته باشد که \(\forall n \in N;\left| {{a_n}} \right| \le k\).
هر دنباله کرانداردارای کران بالا و کران پایین است.
دنباله ای که کراندار نباشد را بی کران گوییم.
هر دنباله همگرا کراندار است.
5- دنباله یکنوا (Monotone sequence)
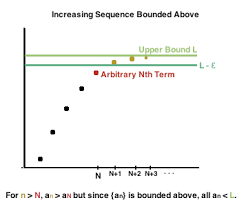
اگر دنبالهای صعودی یا نزولی باشد یکنوا نامیده میشود. اگر دنبالهای اکیداً صعودی یا اکیداً نزولی باشد اکیداً یکنوا نامیده میشود. با مشخص کردن جملات یک دنباله میتوان تشخیص داد که دنباله یکنوا نیست.
دنباله \({a_n}\) را صعودی (صعودی اکید) گوییم هرگاه به ازای هر \(n \in \mathbb{N}\)، داشته باشیم؛ \({a_n} \le {a_{n + 1}}\). یعنی، هر جمله از جمله بعدی کوچکتر یا مساوی باشد.
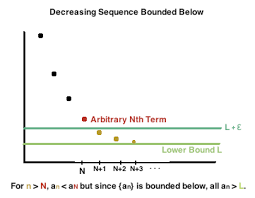
دنباله \({a_n}\) را نزولی (نزولی اکید) گوییم هر گاه به ازای هر \(n \in \mathbb{N}\)، داشته باشیم؛ \({a_{n + 1}} \le {a_n}\). یعنی، هر جمله از جمله بعدی بزرگتر یا مساوی باشد.
بنا به قضیهای داریم هر جمله یکنوا و کراندار همگراست. این قضیه زمانی مورد استفاده است که بخواهیم همگرایی یک دنباله را بررسی کنیم.
6- دنباله حسابی (تصاعد حسابی – Arithmetic sequence)
دنباله حسابی یا تصاعد حسابی (arithmetic progression)، دنباله ای از اعداد است که اختلاف هر دو جمله متوالی آن مقداری ثابت مثلا \(d\) باشد. به این مقدار ثابت، قدر نسبت تصاعد حسابی گفته می شود.
در دنباله حسابی \({a_n}\)، مجموع \(n\) جمله اول را با نماد \({S_n}\) نمایش می دهند و به صورت زیر تعریف می شود:
\({a_1} + {a_2} + {a_3} + \cdots + {a_n} = {S_n}\)اگر \({a_1}\) جمله اول، \({a_n}\) جمله \(n\) ام و\(d\) قدر نسبت دنباله حسابی باشد، مجموع \(n\) جمله اول از رابطه های زیر بدست می آید:
\({S_n} = \frac{n}{2}\left( {{a_1} + {a_n}} \right);or,{S_n} = \frac{n}{2}\left[ {2{a_1} + \left( {n – 1} \right)d} \right]\)
7- دنباله هندسی (تصاعد هندسی – Geometric sequence)
دنباله هندسی یا تصاعد هندسی (geometric progression)، دنباله ای از اعداد است که از جمله اول به بعد هر جمله برابر است با حاصلضرب جمله قبلی در یک عدد ثابت (مخالف صفر و یک) مثلا \(r\). به این مقدار ثابت قدر نسبت تصاعد هندسی گفته می شود.

در دنباله هندسی \({a_n}\)، مجموع \(n\) جمله اول را با نماد \({S_n}\) نمایش می دهند و به صورت زیر تعریف می شود:
\({a_1} + {a_2} + {a_3} + \cdots + {a_n} = {S_n}\)اگر \({a_1}\) جمله اول، \({a_{n + 1}}\) جمله \(\left( {n + 1} \right)\) ام و \(q\) قدر نسبت دنباله هندسی باشد، مجموع \(n\) جمله اول از رابطه های زیر بدست می آید:
\({S_n} = \frac{{{a_1}\left( {1 – {q^n}} \right)}}{{1 – q}} = \frac{{{a_1}\left( {{q^n} – 1} \right)}}{{q – 1}}\)یا
\({S_n} = \frac{{{a_1} – {a_{n + 1}}}}{{1 – q}} = \frac{{{a_{n + 1}} – {a_1}}}{{q – 1}}\)8- دنباله همگرا (Convergence sequence)
اگر \(\mathop {\lim }\limits_{n \to \infty } {a_n} = L\) یعنی، حد دنباله \({a_n}\) وقتی \(n\) به سمت \(\infty \) میل می کند برابر \(L\) باشد آنگاه گوییم دنباله \({a_n}\) به \(L\) همگراست و \({a_n}\) را دنباله ای همگرا می نامیم.
9- دنباله واگرا (Divergent sequence)
اگر برای دنباله \({a_n}\) در تعریف حد دنباله، عدد حقیقی \(L\) وجود نداشته باشد دنباله \({a_n}\) را دنباله ای واگرا می نامیم.
دنباله های واگرا به دو دسته تقسیم می شوند.
10- دنباله فیبوناتچی (Fibonacci sequence)

لئوناردو فیبوناچی (Leonardo Fibonacci) ریاضیدان ایتالیایی است که در سال ۱۲۰۲ با علاقه مندی به این موضوع که اگر یک جفت خرگوش نر و ماده وجود داشته باشد و ویژگی هایی را برای آنها در نظر بگیریم پس از \(n\) ماه چند جفت خرگوش خواهیم داشت؟
ویژگی های که لئوناردو فیبوناتچی در پیدا کردن نتیجه این سوال به عنوان فرضیات مد نظر قرار داده بود به این شرح است:
۱- یک جفت خرگوش نرو ماده تازه متولد شده داریم.
۲- این دو خرگوش پس از یک ماه بالغ می شوند.
۳- دوران بارداری خرگوش ها یک ماه است.
۴- خرگوش ماده پس از رسیدن به سن بلوغ حتما باردار می شود.
۵- نتیجه هر بارداری خرگوش ماده، یک جفت خرگوش نر و ماده است.
۶- خرگوش ها هرگز نمی میرند.
با محاسبه تعداد خرگوش ها در ماه های اول، دوم، سوم و … به نتیجهای دست یافت که امروز آن را با نام دنبال فیبوناتچی میشناسیم. اولین سری این عددها به صورت زیر است:
دنباله فیبوناتچی دنباله ای از اعداد است که در آن به جز دو جمله اول، هر جمله از مجموع دو جمله قبلی بدست می آید و نمایش تابعی آن به صورت زیر است:
1،1،2،3،5،8،13،21،34،55،89،144،233،377،610،987،1597،2584،4181،6765،10946،17711

در این دنباله مشهور یک خاصیت بسیار جالبی که وجود دارد این است که خارج قسمت هر دو جمله متوالی آن، نزدیک به عدد ۱.۶۱۸ است که به آن نسبت طلایی گفته می شود.
این دنباله خواص شگفت انگیز و کاربردهای فراوانی دارد. در جهان گسترده پیرامون نظم خاصی حاکم است که پیشرفت علم، اسرار این نظم را بر همگان آشکار می کند. ریاضیات یکی از علوم پایه و مهم است که به چرایی نظم خاص طبیعت پاسخ می دهد.
یکی از زیباییهای ریاضیات نسبت طلایی (Golden Ratio) است که از اندام انسان گرفته تا آثار برجسته هنر و معماری و همینطور در دانههای گل آفتابگردان رد آن یافت می شود. عدد طلایی یا نسبت طلایی ۱.۶۱۸ حاصل تلاش دانشمندانی چون اقلیدس، لوکاپاچیولی و لئوناردو فیبوناچی است. محققان بر این باور هستند که زیباترین سطوح و اشکال آنهایی است که نسبت طلایی در آنها به کار رفته باشد. اجسام و اشیایی که با این نسبت ساخته می شوند دارای تقارن و زیبایی خاصی هستند که از نظر چشم انسان بسیار زیبا جلوه گر می شوند.
عدد طلایی را معمولا با حرف یونانی “\(\Phi \)” و به صورت زیر نمایش می دهند.
\(\Phi = \frac{{\sqrt 5 + 1}}{2} = 1.618033988749894848204586834366\)
نسبت طلایی در زمینههای زیر یافت میشود:
۱- اگر در پاره خطی، نسبت قسمت بزرگتر به کوچکتر برابر با نسبت کل خط به قسمت بزرگ باشد، این نسبت قطعاً عدد طلایی و برابر ۱.۶۱۸ است.
۲- تعریف دیگر نسبت طلایی: عددی ثابت است که اگر به آن یک واحد اضافه کنیم، به مربع آن خواهیم رسید یعنی، \({a^2} = a + 1\).
۳- تعبیر هندسی مورد فوق، مستطیل طلایی (Golden Rectangle) می باشد که عرض آن یک واحد کمتر از طول آن است.
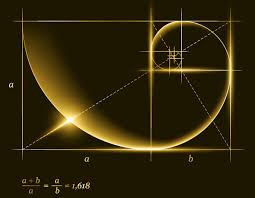
۴- یکی دیگر از حوزههایی که نشانی از نسبت طلایی در آن پیدا میکنید، دنباله فیبوناچی است. در این دنباله که عبارت است از ۱، ۱، ۲، ۳، ۵، ۸، ۱۳، ۲۱ و… اگر اعداد پس از ۲ را در نظر بگیریم و هر کدام را به عدد ماقبل خود تقسیم کنیم، شاهد اعدادی بسیار نزدیک به عدد نسبت طلایی یا ۱.۶۱۸ خواهیم بود. هر چه بیشتر این تقسیم را ادامه دهید، عدد حاصل به نسبت طلایی نزدیکتر میشود.
۵- از مارپیچهای دیانای گرفته تا مارپیچ گوش انسان، حلزون، ساختار مارپیچی کهکشانها و تمام زیباییهای طبیعت ازجمله برگهای درختان، خطوط و نقش و نگار روی پرهای طاووس و مارپیچهای آفتابگردان این نسبت رعایت شده است.


۶- این عدد در معماری باستان و معاصر ایران و جهان نیز کاربرد فراوانی داشته است. از آن جمله میتوان به هرم جیزا در مصر، برج آزادی تهران، قلعه دالاهو در کرمانشاه، بنای بیستون کرمانشاه و مقبره ابن سینا در همدان اشاره کرد. برای مثال ابعاد بنای بیستون کرمانشاه پنج کیلومتر در سه کیلومتر ذکر شده که اعداد چهارم و پنجم دنباله فیبوناچیاند. با تقسیم این دو عدد به عدد ۱.۶ میرسیم که بسیار نزدیک به عدد طلایی است.
۷- این عدد در بدن انسان نیز بسیار کاربرد دارد. زیبایی چهره، زیبایی خنده، تناسب اندام و خوشتیپی همه و همه از شاه کارهای الهی در آفرینش انسان است. اگر نگاهی به تاریخچه عدد طلایی بیندازید، میبینید لئوناردو داوینچی اولین نفری است که نسبت دقیق استخوانهای انسان را اندازهگیری و ثابت کرد این نسبت ضریبی از عدد طلایی است.
۸- در سنجش تناسب اندام خود میتوانید فاصله انگشتان پا تا ناف را بر فاصله ناف تا بالای سر تقسیم و حاصل را با عدد ۱.۶۱۸ مقایسه کنید. هر چه این عدد به ۱.۶۱۸ نزدیکتر باشد به این معنی است که شما تناسب اندام خوبی دارید. چنین نشانههایی که در آنها میتوان به نسبت طلایی رسید، در بدن انسان بسیار زیاد است.
۹- یکی از دیگر ویژگیهای جالب توجه نسبت طلایی این است که اگر فاصله شهر مکه تا قطب شمال را بر فاصله این شهر تا قطب جنوب تقسیم کنیم، عددی بسیار نزدیک به عدد طلایی به دست میآید. بر این اساس میتوان گفت شهر مکه در نقطه طلایی زمین قرار دارد. علاوه بر این، بررسیهای انجام شده نشان داده است شهر مکه در نقطه طلایی عربستان و بنای کعبه در نقطه طلایی شهر مکه قرار دارد.
نسبت فاصله مکه تا قطب جنوب به فاصله آن تا قطب شمال دقیقا برابر ۱٫۶۱۸ است. علاوه بر این نسبت فاصله قطبین به فاصله مکه تا قطب جنوب بار دیگر برابر ۱٫۶۱۸ است.
فاصله مکه تا قطب جنوب=۱۲۳۴۸٫۳۲ کیلومتر
فاصله مکه تا قطب شمال=۷۶۳۱٫۶۸ کیلومتر
با توجه به نقشه ی عرضی و طولی زمین که توسط انسان ها طراحی شده نقطه ی نسبت طلایی زمین در مکه است. نسبت فاصله غرب این نقشه تا مکه به فاصله شرق آن تا مکه باز برابر ۱.۶۱۸ می باشد. علاوه بر این همانطور که در شکل می بینید، نسبت فاصله شرق تا غرب این نقشه به فاصله غرب نقشه تا مکه با کمال شگفتی باز برابر ۱.۶۱۸ می باشد. با توجه به تمام سیستم های نقشه برداری با کمی اختلاف جزئی اندازه گیری نقطه ی نسبت طلایی جهان همواره در محدوده ای از شهر مکه است که کعبه ی مقدس در آن محدوده می باشد.
11- دنباله کُشی (Cauchy Sequence)
دنباله ای است که جملات آن با پیش رفتن دنباله به هم نزدیک و نزدیکتر می شود.
برای دنباله کوشی دو تعریف هم در فضای اعداد حقیقی و هم در فضای متریک داریم که به تعریف هر کدام می پردازیم.
در فضای اعداد حقیقی، دنباله \({a_1},{a_2},{a_3},…\) یک دنباله کوشی است اگر برای هر عدد مثبت دلخواه \(\varepsilon \)، عدد صحیح \(N\) وجود داشته باشد به قسمی که برای تمام \(m,n > N\) داشته باشیم:
\(\left| {{a_m} – {a_n}} \right| < \varepsilon \)در فضای متریک با متریک \(\left( {X,d} \right)\)، دنباله \({a_1},{a_2},{a_3},…\) یک دنباله کوشی است اگر برای هر عدد مثبت دلخواه \(\varepsilon \)، عدد صحیح \(N\) وجود داشته باشد به قسمی که برای تمام \(m,n > N\) داشته باشیم:
\(d\left( {{a_m},{a_n}} \right) < \varepsilon \)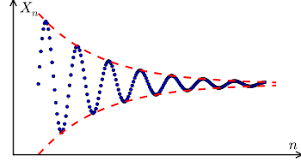
12- دنباله اعداد مثلثی (Triangular Number Sequence)
این دنباله از روی الگوی نقاطی که یک مثلث را تشکیل میدهند، به وجود میآید. با اضافه کردن ردیف دیگری از نقاط و شمارش تمام نقاط در هر مرحله، میتوان عضو بعدی را پیدا کرد.
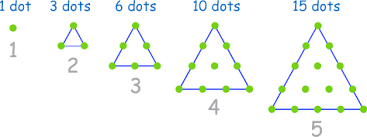
میتوانیم یک «ضابطه» برای این دنباله بنویسیم تا بتوانیم هر عدد مثلثی را به دست بیاوریم. در ابتدا، نقاط را تشکیل میدهیم و به هر الگو یک شماره مانند \(n\) اختصاص میدهیم.

سپس تعداد نقاط را دو برابر میکنیم و شکل آنها را به مستطیل تغییر میدهیم که دارای عرض \(n\) و طول \(n + 1\) هستند. و \({a_n}\) تعداد نقاط در هر مستطیل را مشخص می کند.
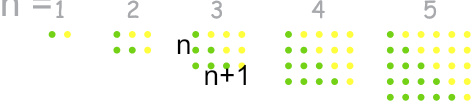
بنابراین با توجه به دو برابر کردن تعداد نقطه ها داریم:
\({a_n} = \frac{{n\left( {n + 1} \right)}}{2}\)همگرایی و عدم همگرایی دنباله
دنباله \({a_n}\) به عدد \(L\) همگرا است اگر به ازای هر \(\varepsilon > 0\)، عدد طبیعی \(N\) وجود داشته باشد به قسمی که \(\forall n \in \mathbb{N}\) و \(n > N\) (از یک جایی به بعد) داشته باشیم:
\(\left| {{a_n} – L} \right| < \varepsilon \)دنبالهای که به هیچ عددی همگرا نباشد دنباله واگرا نامیده میشود. همگرایی دنباله \({a_n}\) به عدد \(L\) معادل تعریف عدد \(L\) بعنوان حد در بینهایت تابعی است که دنباله را تعریف میکند و چون حد تابع در هر نقطه منحصر بفرد است پس، \(L\) یکتاست.
بنا به قضیه ای داریم : هر دنباله یکنوا و کراندار همگرا است ( در این قضیه، هر دو شرط یکنوایی و کرانداری باید همزمان برقرار باشد تا همگرایی نتیجه شود). از مهمترین ویژگیهای دنبالههای همگرا کرانداربودن آنها است. بنابراین دنبالههای همگرا زیر مجموعه ای از مجموعه دنبالههای کراندار هستند.
عکس این مطلب برقرار نیست یعنی مجموعه دنبالههای کراندار زیرمجموعه مجموعه دنبالههای همگرا نیست. با توجه به مطالب بیان شده نتیجه مهم دیگری که میگیریم این است که: هر دنباله همگرا کراندار است اما، ممکن است دنبالهای کراندار باشد ولی همگرا نباشد مانند دنباله \({a_n} = {\left( { – 1} \right)^n}\) که کراندار اما واگرا است. در این مثال، دنباله نوسانی است و یکنوا نیست زیرا به ازای \(n\) های زوج عدد \( +1\) و برای \(n\) های فرد عدد \( – 1\) می شود.
سریها – Series
در ریاضیات، سری اغلب به عنوان مجموع یک دنباله از گزارهها (اعداد یا …) معرفی میشود. در ادامه انواع سری ها رو به تفکیک شرح می دهیم.
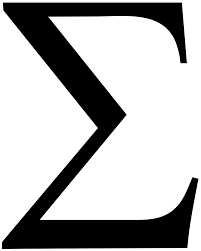
1- سری متناهی (Finite series)
سری های متناهی را می توان با اعمال جبری ساده محاسبه کرد.
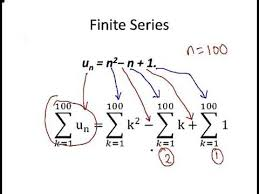
2- سری نامتناهی (Infinite series)
برای محاسبه سری های نامتناهی باید از آنالیز کمک گرفت.

3- سری هندسی (Geometric series)
به مجموع جملات یک دنباله هندسی، سری هندسی گفته می شود و به صورت زیر تعریف می شود:
\(\sum\limits_{k = 0}^n {a{r^k} = a{r^0} + a{r^1} + a{r^2} + \cdots + a{r^n}} \)که در آن \(a\) جمله اول و \(r\) را قدر نسبت سری هندسی می نامند.
4- سری توانی (Power Series)
مجموع \(\sum\limits_{n = 0}^\infty {{a_n}{x^n}} \) را یک سری توانی به مرکز\(0\) و مجموع \({\sum\limits_{n = 0}^\infty {{a_n}\left( {x – c} \right)} ^n}\) را یک سری توانی به مرکز \(c\) گوییم. اگر \({a_n}\) ها اعدادی حقیقی باشند به سری توانی، سری توانی حقیقی گفته می شود.
5- سری همگرا (Convergence Series)
با فرض دنباله \({a_n}\)، دنباله \({S_n}\) مجموع جزئی \(n\) اُمین جمله دنباله ( مجموع جزئی اولین \(n\) جمله اول دنباله) است. به عبارت دیگر:
\({S_n} = \sum\limits_{k = 1}^n {{a_k}} \)یک سری را همگرا گوییم اگر دنباله \({S_1},{S_2},{S_3}, \ldots {\rm{ }}\) به یک مقدار حدی میل کند. به بیان دیگر، یک سری همگراست اگر برای هر عدد مثبت دلخواه و کوچک \(\varepsilon > 0\)، عدد صحیخ و بزرگ \(N\) چنان وجود داشته باشد که
\(\forall n \in N,n \ge N;\left| {{S_n} – l} \right| \le \varepsilon \)
6- سری واگرا (Diverging series)
سری که همگرا نباشد را واگرا گوییم.
7- سری متناوب (Alternate series)
سری \({\sum\limits_{n = 1}^\infty {\left( { – 1} \right)} ^{n + 1}}{a_n}\) را که در آن \({a_n}\) دنباله ای با جملات مثبت، نزولی و همگرا به صفر است یک سری متناوب نامیده می شود.

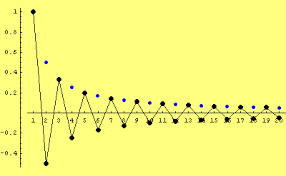
8- سری تلسکوپی (Telescopic Series)

اگر دنباله های \({a_n}\) و \({b_n}\) توسط رابطه \({a_n} = {b_n} – {b_{n + 1}}\) به هم مرتبط باشند و اگر\(\mathop {\lim }\limits_{b \to \infty } {b_n} = b \ne \infty\) وجود داشته باشد آنگاه سری \(\sum\limits_{n = 1}^\infty {{a_n}}\) تلسکوپی نامیده می شود و داریم:
\(\sum\limits_{n = 1}^\infty {{a_n}} = {b_1} – b\)
9- سری با جملات مثبت (Series with positive sentences)
اگر تمام جملات دنباله \({a_n}\) نامنفی باشد آنگاه سری \(\sum\limits_{n = 1}^\infty {{a_n}}\) یک سری با جملات مثبت نامیده می شود.
شرط کُشی برای همگرایی سریها
سری \(\sum\limits_{n = 1}^\infty {{a_n}} \) همگراست اگر و تنها اگر برای هر \(\varepsilon > 0\) عدد طبیعی \(N\) وجود داشته باشد به قسمی که برای هر عدد طبیعی \(n > N\) و هر عدد طبیعی \(p\) داشته باشیم:
\(\left| {{a_{n + 1}} + {a_{n + 2}} + \cdots + {a_{n + p}}} \right| < \varepsilon \)شرط فوق، شرط کشی برای همگرایی سریها است بنابراین اگر سری مذکور همگرا باشد آنگاه؛ \(\mathop {\lim }\limits_{n \to \infty } {a_n} = 0\) و در صورتی که حد گفته شده مخالف صفر باشد آنگاه سری واگرا است.
از این قاعده (شرط کشی)، اغلب برای اثبات واگرایی سریها استفاده میشود. زیرا ممکن است حد جمله عمومی برابر صفر باشد اما سری همگرا نباشد. در واقع، اگر حد مخالف صفر باشد بطور قطع سری واگراست ولی اگر مساوی صفر شد نمیتوان نتیجهای گرفت و باید از آزمونهای مناسب دیگر استفاده کرد.
شعاع همگرایی (The condition of convergence)
فاصله همگرایی یک سری توانی، فاصلهای واقع بین نقاط \( – r\) و \( +r\) است ( یعنی بازه \(\left( { – r, + r} \right)\)) به طوری که به ازای نقاط \( x\) درون این فاصله، سری همگرایی مطلق و به ازای نقاط \(x\) بیرون آن سری واگراست. عدد \( r\) را شعاع همگرایی سری توانی مینامند.
ویژگیهای سری توانی
۱- اگر سری توانی به مرکز صفر، به ازای عددد غیر صفر\(x = {x_1}\) همگرا باشد آنگاه سری مذکور،\(\forall x;\left| x \right| < \left| {{x_1}} \right|\) همگرای مطلق است.
۲- اگر سری توانی به مرکز صفر، به ازای عددد غیر صفر\(x = {x_1}\) واگرا باشد آنگاه سری مذکور، \(\forall x;\left| x \right| > \left| {{x_1}} \right|\) واگرای مطلق است.
۳- سری توانی به مرکز صفر به ازای \(x = 0\) همگرا و به ازای هر مقدار \(x \) همگرای مطلق است.
۴- اگر عدد مثبت \(r\) وجود داشته باشد به قسمی که \(\left| x \right| < r\) آنگاه سری توانی به مرکز صفر همگرای مطلق است و اگر \(\left| x \right| > r\) سری توانی به مرکز صفر واگراست.
قضیه مشتق گیری سری توانی
اگر سری توانی \(\sum\limits_{n = 0}^\infty {{a_n}{x^n}} \) دارای شعاع همگرایی \(r > 0\) باشد، آنگاه شعاع همگرایی سری \(\sum\limits_{n = 0}^\infty {n{a_n}} {x^{n – 1}}\)، که حاصل از مشتق گیری جمله به جمله از سری مذکور است، برابر \(r\) است.
اگر چه قضیه مشتقگیری بیان میکند که مشتق اول سری توانی \(\sum\limits_{n = 0}^\infty {{a_n}{x^n}} \) با شعاع همگرایی غیرصفر وجود دارد اما، چون سری مشتق شده خود یک سری توانی با همان شعاع همگرایی است، از این سری نیز میتوان مشتق گرفت. در نتیجه سری داده شده دو بار مشتقپذیر است. با تکرار این روند، نتیجه میگیریم که همه مشتق های یک سری توانی با شعاع همگرایی \(\left| r \right| \ge 0\) در بازه \(\left( { – r, + r} \right)\) وجود دارند.
قضیه: اگر سری توانی در فاصله \(\left( { – r, + r} \right)\) همگرا باشد، آنگاه مجموع آن سری، نمایشگر تابعی است که در فاصله همگرایی دارای مشتق های تا مرتبه \(n\) ام است، و هر یک از مرتبههای مشتق مثلاً مشتق مرتبه \(n\) ام مجموع سری، برابر مجموع یک سری است که با \(n\) بار مشتقگیری جمله به جمله از سری مفروض بدست می آید. علاوه بر این، فاصله همگرایی هر سری حاصل از مشتقگیری، همان فاصله همگرایی سری مفروض، یعنی \(\left( { – r, + r} \right)\) است.
قضیه انتگرال گیری سری توانی
اگر شعاع همگرایی سری توانی \(\sum\limits_{n = 0}^\infty {{a_n}{x^n}} \)، \(r > 0\) باشد آنگاه شعاع همگرایی سری \(\sum\limits_{n = 0}^\infty {\frac{{{a_n}}}{{n + 1}}} {x^{n + 1}} + c\)، که حاصل از انتگرا گیری جمله به جمله از سری مذکور است، برابر با \(r\) است.
آزمونهای تعیین همگرایی و واگرایی سریها
1- آزمون مقایسه حد
این آزمون بیان میکند که اگر \(\sum\limits_{n = 1}^\infty {{a_n}} \) و \(\sum\limits_{n = 1}^\infty {{b_n}} \) دو سری با جملات مثبت باشند آنگاه اگر \(\mathop {\lim }\limits_{n \to \infty } \frac{{{a_n}}}{{{b_n}}}\) موجود و مخالف صفر باشد دوسری از نظر همگرایی و واگرایی شبیه یکدیگر هستند یعنی هر دو یا واگرا یا همگرا هستند.
2- آزمون مقایسه (Compare test)
آزمون مقایسه از جمله آزمونهایی است که برای تعیین وضعیت همگرایی و واگرایی سریها با جملات حقیقی و مختلط استفاده میشود. اساس کار این آزمون بر پایه مقایسه جملات سری مورد بحث با جملات یک سری است که از وضعیت همگرایی آن اطلاع داریم. پس برای انجام این آزمون نیاز به در نظر گرفتن یک سری دیگر که از وضعیت همگرای آن اطلاع داریم، می باشد. این آزمون به دوصورت انجام می گیرد که به شرح آنها می پردازیم:
الف) آزمون مقایسه نوع اول: این آزمون بیان میکند که اگر \(\sum\limits_{n = 1}^\infty {{b_n}} \) یک سری همگرا باشد و عدد حقیقی \(c\) (غیر وابسته به عدد طبیعی \(n\)) چنان موجود باشد که \(\left| {{a_n}} \right| \le c\left| {{b_n}} \right|\) آنگاه سری \(\sum\limits_{n = 1}^\infty {{a_n}} \) هم همگراست. همچنین اگر \(\sum\limits_{n = 1}^\infty {{b_n}} \) یک سری واگرا باشد و \(\left| {{a_n}} \right| \ge c\left| {{b_n}} \right|\) آنگاه سری \(\sum\limits_{n = 1}^\infty {{a_n}} \) یک سری واگراست.
به طور خلاصه، اگر دوسری \(\sum\limits_{n = 1}^\infty {{a_n}} \) و \(\sum\limits_{n = 1}^\infty {{b_n}} \) داشته باشیم به قسمی که \(\left| {{a_n}} \right| \le \left| {{b_n}} \right|\) آنگاه:
۱- اگر سری \(\sum\limits_{n = 1}^\infty {{b_n}} \) همگرا باشد آنگاه سری \(\sum\limits_{n = 1}^\infty {{a_n}} \) نیز همگراست.
۲- اگر سری \(\sum\limits_{n = 1}^\infty {{a_n}} \) واگرا باشد آنگاه سری \(\sum\limits_{n = 1}^\infty {{b_n}} \) نیز واگراست.
ب) آزمون مقایسه نوع دوم: این آزمون بیان میکند که اگر \(\sum\limits_{n = 1}^\infty {{b_n}} \) یک سری همگرا باشد و عدد حقیقی \(c\) (غیر وابسته به عدد طبیعی \(n\)) چنان موجود باشد که \(\left| {\frac{{{a_{n + 1}}}}{{{a_n}}}} \right| \ge c\left| {\frac{{{b_{n + 1}}}}{{{b_n}}}} \right|\) آنگاه سری \(\sum\limits_{n = 1}^\infty {{a_n}} \) هم همگراست. همچنین اگر \(\sum\limits_{n = 1}^\infty {{b_n}} \) یک سری واگرا باشد و \(\left| {\frac{{{a_{n + 1}}}}{{{a_n}}}} \right| \le c\left| {\frac{{{b_{n + 1}}}}{{{b_n}}}} \right|\) آنگاه سری \(\sum\limits_{n = 1}^\infty {{a_n}} \) یک سری واگراست.
به طور خلاصه، اگر دوسری \(\sum\limits_{n = 1}^\infty {{a_n}} \) و \(\sum\limits_{n = 1}^\infty {{b_n}} \) داشته باشیم به قسمی که \(\left| {\frac{{{a_{n + 1}}}}{{{a_n}}}} \right| \le \left| {\frac{{{b_{n + 1}}}}{{{b_n}}}} \right|\) آنگاه:
۱- اگر سری \(\sum\limits_{n = 1}^\infty {{b_n}} \) همگرا باشد آنگاه سری \(\sum\limits_{n = 1}^\infty {{a_n}} \) نیز همگراست.
۲- اگر سری \(\sum\limits_{n = 1}^\infty {{a_n}} \) واگرا باشد آنگاه سری \(\sum\limits_{n = 1}^\infty {{b_n}} \) نیز واگراست.
3- آزمون نسبت یا قاعده دالامبر( The rule of Dalmeber- Ratio Test)
آزمون نسبت معیاری است برای تعیین وضعیت همگرایی یا واگرایی سریهایی با جملات حقیقی یا مختلط است. این آزمون نخستین بار توسط دالامبر(Jean le Rond d’Alembert) مطرح گردید و به همین دلیل به آن آزمون نسبت دالامبر یا به اختصار آزمون دالامبر میگویند، همچنین این آزمون گاهی با عنوان آزمون نسبت کوشی هم گفته میشود.
اگر \(\sum\limits_{n = 1}^\infty {{a_n}} \) یک سری باشد و نیز داشته باشیم \(L = \mathop {\lim }\limits_{n \to \infty } \left| {\frac{{{a_{n + 1}}}}{{{a_n}}}} \right|\) آنگاه:
۱- اگر\(L < 1\) باشد، آنگاه سری همگراست.
۲- اگر \(L > 1\) باشد، آنگاه سری واگراست.
۳- اگر \(L = 1\) باشد، آنگاه آزمون بی نتیجه است و برای تشخیص وضعیت همگرایی باید از سایر آزمون ها استفاده نمود.

4- آزمون ریشه (Root test)
برای تعیین وضعیت همگرایی سری \(\sum\limits_{n = 1}^\infty {{a_n}} \)، ابتدا حد \(\mathop {L = \lim }\limits_{n \to \infty } \sqrt[n]{{\left| {{a_n}} \right|}} = \mathop {\lim }\limits_{n \to \infty } {\left| {{a_n}} \right|^{\frac{1}{n}}}\) را محاسبه میکنیم. با توجه به مقداری که برای \(L\) بدست خواهد آمد نتایج زیر را میتوان گرفت:
۱- اگر\(L < 1\) باشد، آنگاه سری همگرای مطلق است.
۲- اگر \(L > 1\) باشد، آنگاه سری واگرا است.
۳- اگر \(L = 1\) باشد، آنگاه سری میتواند همگرای مطلق، همگرای مشروط یا واگرا باشد.

5- آزمون انتگرال (Integral test)
آزمون انتگرال از جمله آزمونهای همگرایی سریها است که برای سریهایی با جملات نامنفی کاربرد دارد. این آزمون برای اولین بار در قرن چهاردهم توسط مدهاوا (Madhava) ریاضیدان هندی مطرح شد و بعدها توسط ریاضیدانان اروپایی چون کوشی و مک لورن گسترش پیدا کرد و به همین دلیل گاهی به عنوان آزمون کوشی-مک لورن یا آزمون انتگرال کوشی یا آزمون انتگرال مک لورن، نیز نامیده میشود.
اگر \(\sum\limits_{n = 1}^\infty {{a_n}} \) یک سری نامتناهی باشد و تابع \(f\left( x \right)\) تابعی نزولی و پیوسته در بازه \(\left[ {1,\infty } \right)\) باشد به گونهای که \(f\left( n \right) = {a_n}\) و \(\mathop {\lim }\limits_{x \to \infty } f\left( x \right) = 0\) آنگاه ؛ سری \(\sum\limits_{n = 1}^\infty {{a_n}} \) و \(\int\limits_t^\infty {f\left( x \right)dx} ,1 \le t < \infty \) هر دو از نظر همگرایی مانند هم هستند.



80 Comments
سلام.اثبات اینکه p-سری های همگرا هستند اگر و تنها اگر p>1 چیست؟
سلام بر شما کاربر محترم
همانطور که میدانید p-series(سری فوق هارمونیک)، به صورت مجموعی از ۱ تقسیم بر n^ p است که مقدار n از یک تا بینهایت تعریف میشود. اثبات اینکه p-series برای p بزرگتر از یک همگرا و برای p کوچکتر مساوی یک واگراست در کُتُب و مقاله های متعدد به آن پرداخته شده است برای دسترسی سریعتر، در اینترنت عبارت زیر را سرچ کرده و از لینک های مختلف و نیز ویدئوهای یوتیوب اثبات آن را دریافت کنید.
Proof of p-series convergence criteria
This is the currently selected item.
سلام من تعریف دنباله و سری رو میخوام. شما تعاریف دنباله و سکوینس. رو دارین؟
با سپاس
سلام استاد ببخشید یک سوال داشتم محیط چهار ضلعی نامنظم چیست
سلام بر شما کاربر گرامی
محیط هر شکل هندسی، منظم یا غیر منظم، یعنی دور تا دور شکل.
موفق باشید.
سلام خسته نباشید ببخشید اعمال جبری رویه دنباله ها چیه و درمورد چی توضیح میده؟!
سلام و وقت بخیر
نام چنین دنباله هایی چی هست که بعد از هر چند عدد، عدد ثابت تکرار میشه
3،5،10،7،9،10،11،13،10،15،17
با سلام فرض کنید نقاط a1,a2,a3,…. روی یک خط راست باشند و a1a2=1 و an وسط an+1 و an+2 می باشد. a1a12 چند میشود. اعداد n اندیش هستن
سلام و عرض ادب
بنده فرمول محاسبه لحظه ای حجم یک مخزن استوانه ای افقی با مقطع دوسر مخروط یا دو سر قطاع بیضوی رو میخوام لطفا
سلام خانم فرزامی روز بخیر
در واتساپ براتون پیام گذاشتم لطفاً ملاحظه بفرمایید. با تشکر
با سلام
ببخشید آیا از توالی همرسلی یا نمونه برداری همرسلی اطلاع دارید که چگونه عمل میکند؟
با تشکر
سلام بر شما کاربر محترم
در رابطه با سوال شما اطلاعی ندارم
از مخاطبین و همراهان محترم در صورت دانستن پاسخ سوال، ایشان را راهنمائی بفرمائید متشکرم.
موفق باشید
سلام
می خواستم بدونم چطور میتونم دو سری متناهی رو با هم جمع کنم؟؟؟!!؟
سلام خسته نباشین من دوتا سوال داشتم نمیتونم اثباتش کنم
حد دنباله نزولی و کراندار را مشخص و اثبات کنید
اگر {X n } دنباله عددی باشد کهlim |Xn | موجود است در مورد lim Xn چه می توان گفت.
سلام بر شما کاربر محترم
من تخصصم هندسه هست و سوال شما آنالیزی است.
سوالتون رو برای همکاران به اشتراک میگذارم در صورت دریافت پاسخ در زیر همین پست کامنت خواهم کرد.
ارزوی بهترین ها برای شما
سلام
خسته نباشید
میخواستم بدونم کتاب مرجعی که ساده باشه برای ریاضیات عمومی صرفا برای یادگیری کدوم مورد در دسترس هست؟
و اینکه برای تبدیل ساعت به سال باید چکار کرد؟
مثلا یک میلیارد ساعت چطور میشه بیش از ۱۱۴هزار سال؟
من قصدم اینه ریاضیاتم قوی کنم از پایه، چون یه اطلاعاتی در زندگیم و یسری کتابام هست که مجبورم اینکار کنم.
سلام بر شما کاربر گرامی
متشکرم
ببینید در رابطه با سوال اولی که مطرح فرمودین بایستی مشخص کنید که دقیقا در چه زمینه ای از ریاضیات نیاز به یادگیری جامع دارید زیرا ریاضیات هم مانند سایر علوم طیف گسترده ای از مطالب را شامل است از اینرو تعیین مبحث(به عنوان مثال: هندسه، آنالیز، جبر و…) اولین اقدام برای پیدا کردن و معرفی مرجع مناسب است.
در مورد سوال دوم با بستن دو تناسب ساده به جواب سوالتان خواهید رسید. به این ترتیب که: یک روز معادل 24 ساعت و یک سال معادل 365 روز- بنابراین یکسال معادل 8760 ساعت می باشد. کافیست یک میلیارد ساعت را به 8760 تقسیم کرده و عدد سوالتان را دریافت کنید.
در مورد راهکار های قوی شدن در درس ریاضی بایستی حتما مشاوره شوید بنابراین به شماره ای که در بخش ارتباط با ما است در واتس آپ پیغام بگذارید تا زمان مشاوره متعاقبا خدمتتان اعلام گردد.
با تلاش قطعا موفق میشوید.
سلام خوبین من پایان نامه لازم دارم.
کاربرد دنباله در زندگی روزمره
اگه باشه کتاب معرفی کنی ممنون میشم.
سلام بر شما کاربر محترم
اگر اشتباه نکنم شما بایستی همونی باشین که از کشور افغانستان هستین و امروز در واتساپ هم، پیرامون موضوع پایان نامه ای که ذکر کردین برام پیغام گذاشتین.
اگر بخواهید پایان نامه رو از صفر تا صد خودم براتون بنویسم لازم هستش که تاریخ تحویل و دفاعیه تون رو بهم بگید که بتونم برنامه ریزی کنم.
در حاضر، تایپ پایان نامه سنگین و پر فرموله ای رو دارم از طرفی، حجم کارمم نیز بالاست.
لطفا در واتساپ یا کامنت بهم اطلاع دهید.
آرزوی موفقیت برای شما همراه گرامی
سلام موضوع کاربرد دنباله ها درزندگی روزمره
احسنت به شما
[121√/+…+3√/2+1√/1+1√/1]
سلام
خسته نباشید
این سوال رو بدن انتگرال میشه حل کرد؟
سلام بر شما کاربر محترم
در ابتدا بایستی مجموع دنباله داده شده را محاسبه کنید نتیجه به صورت زیگمای عبارتی خواهد شد.
از طرفی، دنباله ذکر شده در سوال، یک دنباله متناهی است لدا در گرفتن انتگرال زیگما، میتوان جای انتگرال و زیگما را عوض کرد و مقدار انتگرال عبارت را محاسبه کرد
آرزوی موفقیت برای شما.
ممنونم از پاسخ گویی تون
بله مقدار انتگرال اش میشه 20
من منظورم بدون انتگرال یعنی روشی دیگه (معذرت بابت اشتباه تایپی)
خواهش میکنم
شما مقدار انتگرال دنباله مذکور رو محاسبه کردید حالا، بدون انتگرال گرفتن میخواید انتگرال رو محاسبه کنید؟
امکان پذیر نیست.
من منظورم رو نمیتونم انتقال بدم
اصلا انتگرال رو فراموش کنید
الآن که انتگرال از دبیرستان حذف شده یه دانش آموز دبیرستانی نظام جدید چطوری میتونه این سوال رو حل کنه؟
سلام مجدد بر شما
شما بار اول سوال رو به گونه ای مطرح کرده بودین که برداشت من از پرسش شما محاسبه انتگرال دنباله ذکر شده بود.
اما، الان که باز اشاره کردین فکر میکنم سوالتون این بوده که آیا میشه مجموع دنباله فوق رو به کمک انتگرال حل کرد؟
حالا سوال من از شما اینه که چرا به فکرتون رسیده باید به کمک انتگرال حل نمود؟!
بدون نیاز به انتگرال، این سوال قابل حل است.
نوشتن حل این سوال در بخش کامنت سایت سخت می باشد در صورت نیاز در واتساپ به شماره قید شده در قسمت ارتباط با ما سوال خود را مطرح کرده تا در اولین فرصت پاسخ سوال شما را ارسال کنم.
موفق باشید.
سلام بر شما کاربر گرامی
پاسخ سوال شما مخاطب محترم با موضوع مجموع دنباله ذکر شده که در واتساپ هم مطرح فرمودین به زودی در سایت برای رویت سایر همراهان منتشر خواهد شد.
سلام
با راهنمایی استاد فرزامی به کمک استقرا این سوال حل شد
نوشتن تو این قسمت سخته و من از توی ورد کپی کردم این طوری شد (اگه از راست به چپ بخونید شاید مفهوم تر باشه) اگه هم نتونستید بخونید معذرت میخوام
n<√(n+1) □(→┴(+√n ) ) 2√n1/(√(n+1)+√n)→1/(2√n)>√(n+1)-√n√
⟹1/√n>2(√(n+1)-√(n))
1/√1>2√2-2√1
1/√2>2√3-2√2
1/√3>2√4-2√3
.
.
.
1/√121>2√122-2√121
1/√1+1/√2+1/√3+⋯+1/√121>2√122-2√1
1/√1+1/√2+1/√3+⋯+1/√121>20.09
[1/√1+1/√2+1/√3+⋯+1/√121]=20
ولی در کل انتگرال زیبا تر از این هست😂
سلام،
بسيار عالي، استفاده بردم. منتظر مقالات مفيد بعدي شما هستم.
سلام وقت بخیر
جواب این سری چجوری حساب میشه؟
یک دوم منهای یک ششم به علاوه یک دهم منهای یک چهاردهم الی آخر
سلام بر شما کاربر گرامی
لطفا صورت سوالتون رو ایمیل یا در واتس آپ مطرح بفرمائید
سلام. مطلب خیلی کامل و مختصر ومفیدی بود و کمک کننده . خیلی ممنون. موفق باشید.
سلام
متشکرم از حُسن نظر شما به مطالب سایت
امیدوارم مفید واقع شود.
عالی بود واقعا عالی
استاد گرامی با سلام.
از لطف و راهنمائی پر مهر جنابعالی بینهایت ممنونم . و انتظار برآورده شدن لطف مضاعف آن استاد بزرگوار درحق این بنده، برای اصلاح فرمول (زیگما در روش ضرائب استرلینگی، برای حل دنباله های، از نوع ساختمان) خواهم داشت.
با احترام
خواهش میکنم.
به منظور اعمال نظر در مورد فرمول پیشنهادیتان برای حل دنباله مذکور فرصتی مناسب لازم است. اگر نتیجه ای حاصل شد اعلام خواهم کرد.
آرزوی موفقیت
استاد بزرگوار سلام
از جنابتان غیر از این انتظار نمی رفت. و از اینکه با نگاه پر از مهربانی آن استاد معظم سایت حقیر بنده متبرک گردیده با شعف بی پایان بخود می بالم. باور بفرمایید اگر اجباری نداشتم سایت پر از ضعف و اشکالم را خدمت شما استاد گرامی معرفی نمی نمودم.
باسلام خدمت شما
شما به من لطف دارین
روشی که بکار بردین پیچیده هست و زحماتتان قابل ستایش.
در حل یک سوال حتی الامکان میبایست کوتاهترین و بهترین مسیر رو انتخاب نمود.
سوال شما رو خوندم . برای این دنباله تفاضلات که در n امین مرحله از تفاضل گیری های متوالی، قدر نسبت حاصل میشود، جمله عمومی به صورت تابع درجه n است که با جاگذاری n جمله اول در جمله عمومی، یک دستگاه n معادله n مجهول بدست می آید که با روش حذفی راحت تر حل میشود.(من روش حل این مدل دنباله را ساختمان میدانم).
برای نوشتن فرمول مربوطه به صورت زیگما در روش اعداد استرلینگ نیاز به زمان مناسب برای تجزیه و تحلیل است.
لطفا در بخش ارتباط با ما در سایتتون راه ارتباطی قرار دهید.
آرزوی موفقیت روز افزون برای شما
سلام استاد فرهیخته، خانم فرزامی
با عرض خسته نباشید.
دنباله، { … ، 14202، 5861 ، 2029 ، 516 ، 47 ، 38- ، 24- ، 1- } ، از نوع Sixth difference sequences می باشد که در ششمین مرحله از تفاضل گیری های متوالی، مقدار قدر نسبت (60) حاصل می گردد.
سوال بنده اینست که آیا فرمولی برای تعیین جمله ها و نیز محاسبه حاصل جمع جمله ها در دنباله های نظیر مثال فوق و یا دنباله های مرتبه بالاتر و یا پایینتر از آن، ( دنباله هایی که بعد از N مرحله از تفاضل گیری های متوالی قدر نسبت حاصل میگردد) وجود دارد.
بنده فکر می کنم برای آن فرمولی، بر مبنای مجموعه اعداد استرلینگ نوع اول برای Nth difference sequences یافته ام که البته احتیاج به اثبات و اصلاح دارد.
با استفاده از این فرمول کلی، می توان بدون استفاده از محاسبات طولانی و پیچیده، ماتریس و حل دستگاه معادلات، حاصل جمع جمله ها در کلیه دنباله های از نوع مرتبه ای را تعیین نمود.
استاد گرامی، فرمولی کلی را که بنده ( البته فکر می کنم که) ساخته ام، بر اساس مجموعه (اعداد استرلینگ نوع اول) میباشد.
از آنجا که نحوه فشرده سازی فرمول را بلد نیستم و بطور کلی با قوائد استفاده از نماد سیگما ( بخصوص سیگمای دوبل ) برای فشرده سازی فرمول ها آشنایی ندارم .
لذا از آن استاد بزرگوار برای اصلاح و درصورت امکان، اثبات فرمول یاد شده، درخواست راهنمایی و کمک دارم.
بدلیل عدم امکان ارائه فرمول در این صفحه مختصر.
فرمول مورد نظر قبلا به سایت فدیکا email گردیده، و نیز در سایت بنده قابل مشاهده می باشد.
سلام بر شما کاربر محترم
سوالتان را دریافت کردم و سایتتان هم دیدم.
سوال رو بررسی میکنم و نتیجه را در سایت فدیکا خدمتتان اعلام خواهم کرد.
آرزوی موفقیت برای شما
سلام، استاد عالیقدر جناب فرزامی.
با عرض خسته نباشید، به استحضار میرسانم که اینجانب سراجیان اصل از زمان ارسال اولین کامنت به سایت فدیکا، مشتاقانه منتظر پاسخ، و در صورت امکان یاری آن استاد معظم هستم.
آنگونه مشاهده می شود؛ دیگر عزیزان سوال کننده از جنابتان، جواب مناسب دریافت نموده اند، ولی بنده حقیر با وجود اینکه از طریق ارسال ایمیل نیز، شرح بیشتری برای پرسشم ارائه داده ام، هنوز پاسخی نگرفته ام.
که این خود موجب غبطه اینجانب به عزیزان پاسخ گرفته گردیده.
سلام بر شما کاربر محترم
من از شما عذرخواهی میکنم به علت تعویق در پاسخ به سوالتون
لطفا سوالتون رو مجددا ارسال نمائید.
قطعا اگر برای سوالتان هم پاسخی نداشته ام موظف به پاسخگویی بوده ام.😔
با سلام و خسته نباشید و تشکر از سایت خوبتون
میخواستم اگه زحمتی نیست نظرتون رو درباره حل این مسئله بپرسم.
نشان دهید:
هر مجموعه نسبت به خودش بسته و باز است.
R به توان n نسبت به R به توان n+1 بسته است.
سلام استاد و ممنون از این مباحث عالی
جمله هشتم این دنباله رو میشه لطف کنید
2
1
8/9
1
.
.
.
سلام بر شما کاربر محترم
صورت اصلی سوال را در واتساپ ارسال نمائید.
آرزوی موفقیت
سلام استاد گرامی
اگر زحمتی نیست جمله عمومی دو الگوی زیر را بفرمایید.ممنون میشوم.
7،20،47،94،167
و
کسرهای:
11دهم ، یک ، 5ششم،1دوم
ضمنا برای ایجاد مهارت در الگویابی مطلب یا مقاله ای داریم؟
ممنون ، قاسم
سلام بر شما کاربر محترم
متشکرم از توجهتون به سایت فدیکا.
در رابطه با سوالی که مطرح کردین باید بدانید الگویابی، قاعده و قانون مشخصی ندارد به جز الگوهای خاص و یافتن الگو، نیاز به تمرین، تکرار و خلاقیت دارد.
در مثال اول جمله عمومی دنباله به صورت ساختمانی محاسبه میشود.
بدین صورت که شما طی دو مرحله و در سه طبقه رابطه بین هر دو عدد متوالی را به صورت یک جمع رو فلش مربوط مینویسید.
جمله عمومی دنباله به صورت یک چند جمله ای از درجه ۳ است:
A(n)=an^۳+bn^2+cn+d
با تشکیل یک معادله چهار معادله چهار مجهولی(با قرار دادن مقدار n از ۱ تا ۴) خواهیم داشت:
a+b+c+d=7
8a+4b+2c+d=20
27a+9b+3c+d=47
64a+16b+4c+d=94
در نتیجه با حل این دستگاه به یک معادله سه معادله سه مجهولی خواهیم رسید:
7a+3b+c=13
19a+5b+c=27
27a+7b+c=47
با حل این دستگاه به یک دستگاه ۲معادله ۲مجهولی خواهیم رسید:
12a+2b=14
18a+2b=20
در نتیجه از حل این معادله به مقدار 6a=6 و لذا 1=a خواهیم رسید و بنابراین با جایگذاری:
b=1
c=3
d=2
را خواهیم داشت.
در نتیجه جمله عمومی این سوال به صورت زیر خواهد بود.
A(n)=n^3+n^2+3n+2
آرزوی موفقت برای شما.
سلام شاد و سلامت باشین 😊
ببخشین اگه یه دنباله داشته باشیم که فاصلشون یک درمیون یه عدده مثلا این دنباله :
4 ، 7 ،13 ،16 ….
تو این دنباله اختلاف اعداد یک درمیان 6 و 3 هس ، چطوری میتونیم جمله عمومیشو بنویسیم ؟
سلام بر شما کاربرگرامی
در دنباله ذکر شده، با توجه به اینکه اختلاف به صورت یک در میان ۳ و ۶ است.
یعنی دوحالت به وجود آمده است. پس برای حالت زوج و فرد جمله عمومی دنباله را می نویسیم.
در حالت زوج جملات دنباله:
….،۷،۱۶،۲۵
در حالت فرد جملات دنباله:
….،۴،۱۳،۲۲
در هر دو حالت با یک دنباله حسابی روبرو هستیم.
در حالت زوج:
a(n) = a1+(n-1)d
a(n) = 7+(n-1)9
a(n) = 9n-2
در حالت فرد:
a(n) = a1+(n-1)d
a(n) = 4+(n-1)9
a(n) = 9n-5
موفق باشید.
سلام لطفا جمله عمومی دنباله زیر رو بگید
…16 , 0 , 1- ,2-
میشه درباره دنباله های مضلعی توضیح بدین؟
سلام بر شما
دنباله های مضلعی یا اعداد چند ضلعی دنباله هایی هستند که اعداد این دنباله، با شکل چندضلعی های منتظم ارتباط دارند و به چند دسته تقسیم می شوند.
عددهای مثلثی- عددهای مربعی- عددهای پنج ضلعی(مخمسی)-عددهای شش ضلعی(مسدسی)-عددهای هفت ضلعی-عددهای هشت ضلعی
جمله عمومی دنباله های مثلثی:
a(n)=n(n+1)/2
جمله عمومی دنباله های مربعی:
a(n)=n(3n-1)/2
جمله عمومی دنباله های مخمسی:
a(n)=n(2n-1)
سلام
آیا یک رابطه کلی برای بدست آوردن جمله عمومی یا رابطه حاکم بر هر الگوی عددی وجود داره.
منظورم یک رابطه کلیه نه فقط برای دنباله های معروف.
اگه وجود داره میشه اونرو بیان کنید.
با تشکر
سلام بر شما کاربر محترم
جمله عمومی در واقع رابطه بین جملات یه الگو(دنباله یا تصاعد) را بیان می کند بدست آوردن این رابطه نیاز به خلاقیت، تمرکز، دقت، و محاسبات ریاضی دارد.
در برخی از الگوها، پس از بررسی های انجام شده میان اعضای آن، به رابطه مشخصی برای جمله عمومی آن رسیده اند مثل دنباله های معروف فیبونتاچی، هندسی، حسابی و…
اما این موضوع دال بر این نیست که سایر الگوها نیز باید رابطه تعریف شده ای از قبل داشته باشند. لذا لازم است که این موضوع کنکاش گردد.
موفق و پیروز باشید.
باسلام و وقت بخیر
میبخشید سوالی داشتم که ممنون می شوم من رو راهنمایی کنید
دنباله زیر
….1.2.2.3.3.3.4.4.4.4
الف) اسم این نوع دنباله ها چیست؟
ب) فرمول آن چیست؟
ج) جمله چهلم این دنباله چند است ؟
بسیار سپاس گذارم
سلام استاد فرهیخته، جناب فرزامی
با عرض خسته نباشید
از دنباله، { … ، 1402، 5861 ، 2029 ، 516 ، 47 ، 38- ، 24- ، 1- } ، بعد از منها نمودن های متوالی ، (هر جمله منهای جمله قبلی) دنباله دیگری حاصل میگردد؛ و بر این منوال، آن دنباله نیز دنباله دیگری را حاصل می نماید و در ادامه این پروسه ( ایجاد دنباله از دنباله مرتبه بالا تر ) در مرحله هفتم مقدار قدر نسبت ( 60 ) بدست می آید. به این نوع دنباله ها که طی چند مرحله از تفاضل گیری مقدار قدر نسبت حاصل می شود Nth difference sequences می گویند . ( با عرض پوزش از محضر استاد فرزانه، جهت درس پس دادن ناقص)
سوال بنده اینست که آیا فرمول و یا روش شناخته شده ای برای محاسبه حاصل جمع، بطور مثال، چهل جمله اول از دنباله فوق وجود دارد؟
بنده فکر می کنم فرمولی کلی و ساده ای ، بر مبنای ضرایب اعداد استرلینگ برای Nth difference sequences یافته ام که احتیاج به اثبات و اصلاح دارد. نظر و یاری شما استاد گرامی را مسئلت دارم.
سلام
در دنباله ی ۳،۵،۸،۱۲،۱۷ جمله ی چهلم چند میشه؟فرمولش چیه؟ممنون
سلام بر شما کاربر گرامی
دنباله ای که شما مطرح کردین نه دنباله حسابی است و نه دنباله هندسی. برای اینکه دنباله ای حسابی باشد میبایست هر جمله(از جمله دوم به بعد) از جمع جمله قبلی با یک عدد ثابت بدست آید و از طرف دیگر دنباله ای هندسیست که هر جمله(از جمله دوم به بعد) از ضرب جمله قبل در یک عدد ثابت بدست آید. در اینجا قدر نسبت عددی ثابت نیست و جمله عمومی چنین دنباله ای یک جمله درجه ۲ میباشد در حالیکه در دنباله های حسابی با توجه به فرمول ذکر شده در مورد آنها میبینیم که جمله عمومی از درجه یک میباشد.
و اما حل سوال؛
جمله عمومی را به صورت یک معادله درجه دو می نویسیم سپس، با قرار دادن n=1 و n=2 وn=3 به جای n در فرم درجه دو به یک دستگاه سه معادله سه مجهول میرسیم:
3=a+b+c
4a+2b+c=5
9a+3b+c=8
از حل این دستگاه به جواب a=b=1/2 و c=2 می رسیم بنابراین:
در جمله عمومی دنباله که به فرم درجه ۲ هست ضرایب ثابت بدست امده را جایگذاری میکنیم سپس با قرار دادن n=40 در این معادله که در واقع جمله عمومی دنباله هست به مقدار جمله چهلم که مساوی۸۲۲ است دست پیدا میکنیم.
با سلام و درود به استادان گرانقدر ریاضی این سرزمین …سپاس از تلاش شما عزیزان که این آموخته ها را در این site بارگزاری کردید
درود بر شما
متشکرم از قدردانی شما
سلام خدمت شما
خیلی ممنون. سایتتون واقعا پر محتوا و زیباست. من خیلی سایتتون رو دنبال می کنم. کاش راجع به جایگشت ها و ترکیبات، نسبتهای مثلثاتی هم مطلب قرار میدادین.
براتون آرزوی موفقیت میکنم خانم دکتر
درود بر شما
متشکرم از حُسن نظرتون و اینکه سایت ما رو دنبال میفرمائید.
حقیقتش به چند دلیل مطلب جدید اضافه نکردم
۱- کوتاهی کردن در زمان هایی که فرصت داشتم
۲-مشغله کاری
۳- مشکل فنی سیستمم
انشالله سیستمم رو درست کنم در مورد مثلثات مقاله ام تکمیل و منتشر میکنم و مقالات متعدد دیگری رو هم خواهم گذاشت.
موفق باشید
سلام استاد.
بنده پیرمردی 63 ساله، در مقابل علمی جنابعالی بیسوادی بیش نیستم ( دیپلمه طبیعی ) فرمولی (من درآوردی) برای محاسبه حاصل جمع جمله های دنباله های حسابی با ویژگی تفاضل گیری چند مرحله ای برای رسیدن به مقدار قدر نسبت ( مثلا درست کردم ) ولی از نماد سیگما در آن فرمول، استفاده نادرست نمودم ( مثل بار یک کامیون را در یک وانت کوچک جای دادن) در فرمول، چند مقدار ثابت و متغیر را بعنوان مقادیر معلوم یک نماد سیگما نشان دادم (که میدانم مجاز نیست ) از نماد سیگمای دوبل هم بلد نیستم استفاده نمایم.
آیا راهی برای اصلاح چنین فرمولی هست ؟
سلام بر شما کاربر محترم
متشکرم از حُسن توجه شما به مطالب سایت.
و البته هر آنچه که آموخته ایم در حیطه فعالیتمان، قبل از تلاش خودمان، از آموزش خوب و انگیزش افراد با تجربه و باسوادی در سن شما پدر بزرگوار است.
سوالتون رو متوجه نشدم
متوجه نشدم در فرمول محاسبه مجموع اعضای دنباله حسابی برای بدست اوردن قدر نسبت دنباله چه تغییراتی اعمال کردید و هدفتان چیست؟! لطفا سوالتان را واضح تر در همین جا و یا از طریق راه های ارتباطی دیگر که در صفحه “تماس با ما” است مطرح بفرمائید تا بتوانم در صورت امکان کمکتان کنم.
استاد بزرگوار.
با تشکر از حسن ظن جنابعالی بعرض می رسانم که بنده فرمول مورد نظر را خدمتتان ایمیل نموده ام و بار دیگر آنرا ارسال می دارم . البته حقیر یک وب سایت برای ارائه نوشته هایم دارم که البته می دانم معرفی آن به شما استاد بزرگ در حکم نشان دادن نقاشی کودکانه به بزرگان نقاشی می باشد.
باری چاره ای از آن نیست .مشکل اینجانب نحوه نوشتن نماد سیگما برای چهار مقدار مرتبط، ” n ” شماره ردیف افقی مجموعه استرلینگ، ” k ” شماره ردیف عمودی مجموعه استرلینگ، ” f ” مرتبه دنباله برای رسیدن به تفاضل مشترک ، ” t ” تعداد جمله های حاصل جمع از دنباله.
سلام
از شما خانم محترم، به خاطر نشر این مطالب مفید به گونه ای قابل فهم و خلاصه و جامع واقعا تشکر می کنم. احسنت بر شما
توی وب های فارسی زبان همچین مطالبی رو پیدا کردن خیلی قابل تقدیر هست…تشکر
سلام خیلی عالیه مطالبتون
سوالی داشتم از خدمتتون
درباره حد و پیوستگی کتابی متفاوت از کتابهای موجود در بازار وجود داره که هم خیلی خوب درس داده باشه و هم سوالهای جذابی داشته باشه؟
باسلام خانم دکترفرزامی ,مطالب بسیارمفیدوکاربردی هستندموفق باشید.
سلام بر شما مخاطب گرامی
از حُسن نظر شما سپاسگزارم.
با سلام خانم فرزامی بخاطر سایت خوب و مفیدتون تبریک میگم بنده هم دانشجوی دکتری شهید مدنی هستم تلاشتون جای تقدیر و تشکر داره موفق باشید
محمودی
سلام جناب محمودی
متشکرم از حسن نظرتون
از اینکه از مطالب سایت بازدید و رضایت داشتید خرسندم.
میشه این سوال را جواب بدید ۱-۵-۷-۱۳-۲۵ میشه رابطه رو بگید ممنون
سلام
به سوالتون پاسخ میدم حتما
اگر صورت اصلی سوال رو هم عکس بگیرید و در واتساپ ارسال کنید خوبه.
پست موقت می باشد.
دستت درد نکنه خانم فرزامی
چند سالی بود از ریاضیات فاصله گرفته بودم ، روح تازه ای در رگهام جاری شد ….سری ها هندسی خیلی دوست داشتم
خواهش میکنم آقا سلیم
خوشحالم از اینکه مطالب برای شما در خور توجه بوده.
سلام لطفا کتابی در زمینه جبر برای دانشگاه معرفی نمایید
سلام کتاب در مورد سری ها و دنباله ها در سطح دانشگاه میخوام
سلام بر شما آقای احمد زاده
در مورد سوال شما، از انجایی که سوال دیگرانی چون شما نیز است بزودی حتما مقاله یا کتابی را معرفی خواهم نمود.