تاریخچه هندسه

هندسه ((به یونانی: γεωμετρία)، ژئو«زمین»، مترون «اندازهگیری») شاخهای ازریاضیات است که با شکل، اندازه، موقعیت نسبی اشکال و ویژگیهای فضا سروکار دارد. ریاضیدانی که در شاخه هندسه کارمیکند هندسه دان نامیده میشود.هندسه به طورمستقل در پارهای از تمدنهای اولیه به شکل بدنهای از دانش عملی در مورد طول، مساحت و حجم ظهور کرد و پایهریزی آن به عنوان یک دانش رسمی ریاضی در زمان تالس (قرن ششم پیش از میلاد) آغاز شد.
در قرن سوم پیش از میلاد هندسه توسط اُقلیدس به شکل اصل موضوعی درآمده بود و کار اُقلیدس – هندسه اُقلیدسی – استانداردی را پایهریزی نمود که قرنها دنبال شد.
ارشمیدس روشهای هوشمندانهای برای محاسبهٔ مساحت و حجم ارائه داد که در بسیاری موارد پیشرو حساب انتگرال جدید محسوب میشوند. دانش اخترشناسی و به ویژه نگاشتن مکان ستارهها و سیارهها روی کرهی آسمان و توصیف رابطهی بین حرکت اجسام آسمانی تا هزار و پانصد سال بعد منشأ بسیاری از پرسشهای هندسی بود. به احتمال زیاد ، بابلیان و مصریان کهن نخستین کسانی بودند که اصول هندسه را کشف کردند.
در مصر هر سال رودخانه نیل طغیان میکرد و نواحی اطراف رودخانه را سیل فرا میگرفت. این رویداد تمام علایم مرزی میان املاک را از بین میبرد و لازم میشد دوباره هر کس زمین خود را اندازهگیری و مرزبندی کند.
مصریان روش علامتگذاری زمینها با تیرک و طناب را ابداع کردند. آنها تیرکی را در نقطهای مناسب در زمین فرومیکردند و تیرک دیگری در جایی دیگر نصب میشد و دو تیرک با طنابی که مرز را مشخص میساخت به یکدیگر متصل میشدند. با دو تیرک دیگر زمین محصور شده و محلی برای کشت یا ساختمان سازی مشخص میشد.
در آغاز هندسه بر پایهی دانستههای تجربی پراکندهای در مورد طول و زاویه و مساحت و حجم قرار داشت که برای مساحی(اندازه گرفتن سطح زمین) و ساختمان و نجوم و برخی صنایع دستی لازم میشد.
یونانیان دانستههای هندسی را مُدَوّن کردند و بر پایهای استدلالی قراردادند. برای آنان هندسه، مهمترین دانشها بود. در سال ۶۰۰ قبل از میلاد مسیح، یک آموزگار اهل ایونیا (که در روزگار ما بخشی ازترکیه به شمار میرود) به نام تالس، چند گزاره یا قضیهی هندسی را به صورت استنتاجی ثابت کرد. او آغازگر هندسهی ترسیمی بود.
روش استنتاجی روشی است علمی (بر خلاف روش استقرایی) که در آن مسئلهای به وسیلهی قضایا و حکمها ثابت میگردد. فیثاغورث که او نیز اهل ایونیا و احتمالاً از شاگردان تالس بود توانست قضیهای را که به نام او مشهور است اثبات ریاضی کند.
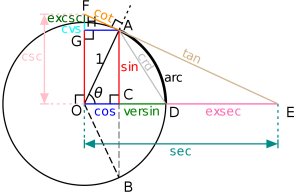
هندسهی اُقلیدسی- توابع
اما دانشمندی به نام اُقلیدس که در اسکندریه زندگی میکرد، هندسه را به صورت یک علم بیان نمود. وی حدود ۳۰۰ سال پیش از میلاد مسیح، تمام نتایج هندسی را که تا آن زمان شناخته بود، گرد آورد و آنها را به طور منظم، در یک مجموعهی ۱۳ جلدی قرارداد.
این کتابها که اصول هندسه نام داشتند، به مدت ۲ هزار سال در سراسر دنیا برای مطالعهی هندسه به کار میرفتند. بر اساس این قوانین، هندسهی اُقلیدسی تکامل یافت. هر چه زمان میگذشت، شاخههای دیگری از هندسه توسط ریاضیدانان مختلف، توسعه مییافت.
خدمت بزرگی که یونانیان در پیشرفت ریاضیات انجام دادند این بود که آنها احکام ریاضی را به جای تجربه بر استدلال منطقی استوار کردند. قبل ازاُقلیدس، فیثاغورث و زنون نیز به پیشرفت علم ریاضی خدمت بسیار کرده بودند. در قرن دوم قبل از میلاد ریاضیدانی به نام هیپارک، مثلثات را اختراع کرد. وی نخستین کسی بود که تقسیمبندی بابلیها را برای پیرامون دایره پذیرفت.
تقسیم بندی انواع هندسه
هندسه مقدماتي به دو قسمت تقسيم ميگردد: هندسه مسطحه و هندسه فضايي
در هندسه مسطحه، اشکالي مورد مطالعه قرار ميگيرند که فقط دو بعد دارند. درهندسه فضايي، مطالعه اشکال هندسي سه بعدي را داریم. اين بخش از هندسه در مورد اشکال سه بعدي چون مکعبها ،استوانهها، مخروطها، کرهها و… است.
در هندسه مدرن شاخههای زیر مورد مطالعه قرار میگیرند:
1- هندسه تحلیلی
2- هندسه برداری
3- هندسه دیفرانسیل
4- هندسه جبری
5- هندسه محاسباتی
6- هندسه اعداد صحیح
7- هندسه اُقلیدسی
8- هندسه نااُقلیدسی
9- هندسه تصویری
10- هندسه ریمانی
11- هندسه ناجابجایی
12- هندسه هذلولوی
هندسه اُقلیدسی و انحنای فضا
علومي كه از يونان باستان توسط انديشمندان اسلامي محافظت و تكميل شد، از قرون يازدهم ميلادي به بعد به اروپا منتقل شد و بيشتر شامل رياضي و فلسفه ي طبيعي بود.
فلسفه ي طبيعي توسط كوپرنيك، برونو، كپلر و گاليله به چالش كشيده شد و از آن ميان فيزيك نيوتني بيرون آمد. چون كليسا خود را مدافع فلسفه طبيعي يونان مي دانست و كنكاش در آن با خطرات زيادي همراه بود، انديشمندان كنجكاو بيشتر به رياضيات ميپرداختند، زيرا كليسا نسبت به آن حساسيت نشان نميداد. بنابراين رياضيات نسبت به فيزيك از پيشرفت بيشتري برخوردار بود. يكي از شاخه هاي مهم رياضيات هندسه بود كه آن هم درهندسهي اُقليدسي خلاصه ميشد.
درهندسهي اُقليدسي يك سري مفاهيم اوليه نظيرخط و نقطه تعريف شده بود و پنچ اصل را به عنوان بديهيات پذيرفته بودند و ساير قضايا را با استفاده از اين اصول استنتاج ميكردند. اما اصل پنجم چندان بديهي به نظر نميرسيد. بنابراصل پنجم اُقليدس از يك نقطه خارج از يك خط، يك خط و تنها يك خط ميتوان موازي با خط مفروض رسم كرد.
برخي از رياضيدانان مدعي بودند كه اين اصل را ميتوان به عنوان يك قضيه ثابت كرد. در اين راه بسياري از رياضيدانان تلاش زيادي كردند و نتيجه نگرفتند. خيام ضمن جستجوي راهي براي اثبات اصل توازي مبتكر مفهوم عميقي درهندسه شد.
برخي از رياضيدانان مدعي بودند كه اين اصل را ميتوان به عنوان يك قضيه ثابت كرد. در اين راه بسياري از رياضيدانان تلاش زيادي كردند و نتيجه نگرفتند. خيام ضمن جستجوي راهي براي اثبات اصل توازي مبتكر مفهوم عميقي درهندسه شد.
در تلاش براي اثبات اين اصل، خيام گزارههايي را بيان كرد كه كاملاً مطابق گزارههايي بود كه چند قرن بعد توسط واليس و ساكري رياضيدانان اروپايي بيان شد و راه را براي ظهور هندسههاي نااُقلیدسی در قرن نوزدهم هموار كرد. سرانجام و پس از دو هزار سال اصولي متفاوت با آن بيان كردند و هندسههاي نااُقلیدسی شكل گرفت. بدين ترتيب علاوه بر فلسفهي طبيعي رياضيات نيز از انحصار يوناني خارج و در مسيري جديد قرار گرفت و آزاد انديشي در رياضيات آغاز گرديد.
اصطلاحات بنیادی ریاضیات
طي قرنهاي متمادي رياضيدانان اشياء و موضوعهاي مورد مطلعهي خود از قبيل نقطه و خط وعدد را هم چون كميتهايي در نظر ميگرفتند كه درنفس خويش وجود دارند. اين موجودات همواره همهي كوششهاي را كه براي تعريف و توصيف شايستهي آنان انجام ميشد را با شكست مواجه ميساختند. به تدريج اين نكته بر رياضيدانان قرن نوزدهم آشكارگرديد كه تعيين مفهوم اين موجودات نمي تواند در داخل رياضيات معنايي داشته باشد. حتي اگر اصولاً داراي معنايي باشند.
بنابراين، اينكه اعداد، نقطه و خط در واقع چه هستند در علوم رياضي نه قابل بحث است و نه احتياجي به اين بحث هست. يكبارراسل گفته بود كه رياضيات موضوعي است كه در آن نه ميدانيم از چه سخن ميگوييم و نه ميدانيم آنچه كه ميگوييم درست است.
دليل آن اين است كه برخي از اصطلاحات اوليه نظير نقطه، خط و صفحه تعريف نشده اند و ممكن است به جاي آنها اصطلاحات ديگري بگذاريم بي آنكه در درستي نتايج تاثيري داشته باشد. مثلاً ميتوانيم به جاي آنكه بگوييم دو نقطه فقط يك خط را مشخص مي كند، مي توانيم بگوييم دو آلفا يك بتا را مشخص ميكند.
با وجود تغييري كه در اصطلاحات داديم، باز هم اثبات همهي قضاياي ما معتبر خواهد ماند، زيرا كه دليلهاي درست به شكل نمودار بسته نيستند، بلكه فقط به اصول موضوع كه وضع شده اند و قواعد منطق بستگي دارند..
بنابراين، رياضيات تمريني است كاملاً صوري براي استخراج برخي نتايج از بعضي مقدمات صوري. رياضيات احكامي مي سازند به صورت هرگاه چنين باشد، آنگاه چنان خواهد شد و اساساً در آن صحبتي از معني فرضها يا راست بودن آنها نيست. اين ديدگاه (صوريگرايي) با عقيدهي كهن تري كه رياضيات را حقيقت محض ميپنداشت و كشف هندسههاي نااُقلیدسی بناي آن را درهم ريخت، جدايي اساسي دارد. اين كشف اثر آزادي بخشي بر رياضيدانان داشت.
اشكالات وارد بر هندسه اُقليدسي
هندسهي اُقليدسي بر اساس پنچ اصل موضوع زير شكل گرفت:
اصل اول – از هر نقطه مي توان خط مستقيمي به هر نقطه ي ديگر كشيد.
اصل دوم – هر پاره خط مستقيم را ميتوان روي همان خط به طور نامحدود امتداد داد.
اصل سوم – ميتوان دايرهاي با هر نقطه دلخواه به عنوان مركز آن و با شعاعي مساوي هر پاره خط رسم كرد.
اصل چهارم – همه ي زواياي قائمه با هم مساوي اند.
اصل پنجم – از يك نقطه خارج يك خط، يك خط و تنها يك خط ميتوان موازي با خط مفروض رسم كرد.
اصل پنجم اُقليدس كه ايجاز ساير اصول را نداشت، به هيچوجه واجد صفت بديهي نبود. در واقع اين اصل بيشتر به يك قضيه شباهت داشت تا به يك اصل. بنابراين طبيعي بود كه لزوم واقعي آن به عنوان يك اصل مورد سوال قرار گيرد. زيرا چنين تصور ميشد كه شايد بتوان آن را به عنوان يك قضيه نه اصل از ساير اصول استخراج كرد، يا حداقل به جاي آن ميتوان معادل قابل قبول تري قرار داد.
در طول تاريخ رياضيدانان بسياري از جمله، خواجه نصيرالدين طوسي، جان واليس، لژاندر، فوركوش بويوئي و … تلاش كردند اصل پنجم اُقليدس را با استفاده از ساير اصول نتيجه بگيرند و آن را به عنوان يك قضيه اثبات كنند. اما تمام تلاشها بي نتيجه بود و در اثبات دچار خطا ميشدند و به نوعي همين اصل را در اثبات خود به كارميبردند. دلامبر اين وضع را افتضاح هندسه ناميد.
يانوش بويوئي يكي ازرياضيدانان جواني بود كه در اين راه تلاش ميكرد. پدر وي نيز رياضيداني بود كه سالها در اين مسير تلاش كرده بود و طي نامهاي به پسرش نوشت: تو ديگر نبايد براي گام نهادن در راه توازيها تلاش كني، من پيچ و خم اين راه را از اول تا آخر ميشناسم. اين شب بي پايان همه روشنايي و شادماني زندگي مرا به كام نابودي فرو برده است، التماس مي كنم دانش موازيها را رها كني.
ولي يانوش جوان از اخطار پدر نهراسيد، زيرا كه انديشهي كاملاً تازه اي را در سر ميپروراند. او فرض كرد نقيض اصل توازي اُقليدس، حكم بي معنياي نيست. وي در سال 1823 پدرش را محرمانه در جريان كشف خود قرار داد و در سال 1831 اكتشافات خود را به صورت ضميمه در كتاب تنتامن پدرش منتشر كرد و نسخهاي از آن را براي گاوس فرستاد.
بعدها معلوم شد كه گاوس خود مستقلاً آن را كشف كرده است. بعدها مشخص شد كه لباچُفسكي در سال 1829 كشفيات خود را در باره هندسهی نااُقلیدسی در بولتن كازان، دو سال قبل از بوئي منتشر كرده است. و بدين ترتيب كشف هندسههای نااُقلیدسی به نام بويوئي و لباچُفسكي ثبت گردي.
هندسه هاي نااُقليدسي
اساساً هندسه نااُقلیدسی چيست؟ هر هندسهاي غيرازاُقليدسي را نااُقليدسي مينامند. از اين گونه هندسهها تا به حال زياد شناخته شده است. اختلاف بين هندسههاي نااُقليدسي واُقليدسي تنها دراصل توازي است. در هندسه اُقليدسي به ازاي هر خط و هر نقطه ناواقع بر آن يك خط مي توان موازي با آن رسم كرد.
نقيض اين اصل را به دو صورت ميتوان در نظر گرفت. تعداد خطوط موازي كه از يك نقطه نا واقع بر آن، ميتوان رسم كرد، بيش از يكي است و يا اصلا خطوط موازي وجود ندارند. با توجه به اين دو نقيض، هندسههاي نااُقليدسي را ميتوان به دو گروه تقسيم كرد.
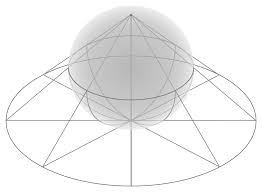
يك – هندسههاي هذلولوي
هندسههاي هذلولوي توسط بويوئي و لباچُفسكي بطورمستقل و همزمان كشف گرديد.
اصل توازي هندسه هذلولوي- از يك خط و يك نقطه ي نا واقع برآن دست كم دو خط موازي با خط مفروض ميتوان رسم كرد.
دو – هندسههاي بيضوي
در سال 1854 فريدريش برنهارد ريمان نشان داد كه اگر نامتناهي بودن خط مستقيم كنار گذاشته شود و صرفاً بيكرانگي آن مورد پذيرش واقع شود، آنگاه با چند جرح و تعديل جزئي اصول موضوعه ديگر، هندسه سازگار نااُقلیدسی ديگري را مي توان به دست آورد. پس از اين تغييرات اصل توازي هندسه بيضوي بصورت زير ارائه گرديد.
اصل توازي هندسه بيضوي – از يك نقطه ناواقع بر يك خط نميتوان خطي به موازات خط مفروض رسم كرد.يعني در هندسه بيضوي، خطوط موازي وجود ندارد. با تجسم سطح يك كره مي توان سطحي شبيه سطح بيضوي در نظر گرفت. اين سطح كروي را مشابه يك صفحه در نظر ميگيرند. در اينجا خطوط با دايرههاي عظميه كره نمايش داده مي شوند. بنابراين خط ژئودزيك يا مساحتي در هندسه بيضوي بخشي از يك دايره عظيمه است.
در هندسه بيضوي مجموع زواياي يك مثلث بيشتر از 180 درجه است. در هندسه بيضوي با حركت از يك نقطه و پيمودن يك خط مستقيم در آن صفحه، مي توان به نقطه ي اول باز گشت. همچنين ميتوان ديد كه درهندسه بيضوي نسبت محيط يك دايره به قطر آن همواره كمتر از عدد پي است.
انحناي سطح يا انحناي گاوسي
اگر خط را راست فرض كنيم، نه خميده، چنانچه ناگزيرباشيم يك انحناي عددي k به خطي نسبت دهيم براي خط راست خواهيم داشت k=0. انحناي يك دايره به شعاع r برابر است با k=1/r تعريف مي كنند. همچنين منحني هموار، منحنياي است كه مماس بر هر نقطه اش به بطور پيوسته تغيير كند. به عبارت ديگر منحني هموار يعني در تمام نقاطش مشتق پذير باشد. براي به دست آوردن انحناي يك منحني در يك نقطه، دايره بوسان آن را درآن نقطه رسم كرده، انحناي منحني در آن نقطه برابر با انحناي دايره ي بوسان در آن نقطه است.
دايره بوسان در يك نقطه از منحني، دايرهاي است كه در آن نقطه با منحني بيشترين تماس را دارد. توجه شود كه براي خط راست شعاع دايره بوسان آن درهر نقطه واقع برآن بينهايت است.
براي تعيين انحناي يك سطح در يك نقطه، دو خط متقاطع مساحتي در دو جهت اصلي در آن نقطه انتخاب كرده و انحناي اين دو خط را در آن نقاط تعيين ميكنيم. فرض كنيم انحناي اين دو خط
K1=1/ R1 and k2=1/ R2
باشند. آنگاه انحناي سطح در آن نقطه برابر است با حاصلضرب اين دو انحنا، يعني :
k=1/ R1R2
انحناي صفحه ي اُقلیدسی صفراست. همچنين انحناي استوانه صفر است:
k=0
براي سطح هذلولوي همواره انحناي سطح منفي است :
k<0
براي سطح بيضوي همواره انحنا مثبت است :
k>0

مفهوم و درك شهودي انحناي فضا
سوال اساسي اين است كه كدام يك از اين هندسههاي اُقليدسي يا نااُقليدسي درست است؟
پاسخ صريح و روشن اين است كه بايد انحناي يك سطح را تعيين كنيم تا مشخص شود كدام يك درست است. بهترين دانشي كه ميتواند در شناخت نوع هندسهي يك سطح مورد استفاده و استناد قرار گيرد، فيزيك است. يك صفحهي كاغذ برداريد و در روي آن دو خط متقاطع رسم كنيد سپس انحناي اين خطوط را در آن نقطه تعيين كرده و با توجه به تعريف انحناي سطح حاصلضرب آن را به دست ميآوريم. اگر مقدار انحنا برابر صفر شد، صفحه اُقليدسي است، اگر منفي شد ميگوييم صفحه هذلولوي است و در صورتي كه مثبت شود، ادعا مي كنيم كه صفحه بيضوي است .
در كارهاي معمولي مهندسي نظير ايجاد ساختمان يا ساختن يك سد بر روي رودخانه، انحناي سطح مورد نظر برابر صفر است، به همين دليل در طول تاريخ مهندسين همواره از هندسهی اُقليدسي استفاده كرده اند و با هيچگونه مشكلي هم مواجه نشدهاند. يا براي نقشه برداري از سطح يك كشور اصول هندسهی اُقليدسي را بكار ميبرند و فراز و نشيب نقاط مختلف آن را مشخص ميكنند.
در اين محاسبات ما ميتوانيم از خطكشهايي كه در آزمايشگاه يا كارخانهها ساخته ميشود، استفاده كنيم. حال سوال اين است كه اگر خطكش مورد استفادهي ما تحت تاثير شرايط محيطي قراربگيرد چه بايد كرد؟ اما ميدانيم از هر ماده اي كه براي ساختن خطكش استفاده كنيم، شرايط فيزيكي محيط بر روي آن اثر ميگذارد. البته با توجه با تاثير محيط بر روي خطكش ما تلاش ميكنيم از بهترين مادهي ممكن استفاده كنيم. به همين دليل چوب از لاستيك بهتر است و آهن بهتر از چوب است.
اما براي مسافتهاي دور نظير فواصل نجومي از چه خطكشي (متري) مي توانيم استفاده كنيم؟ طبيعي است كه در اينجا هيچ خطكشي وجود ندارد كه بتوانيم با استفاده از آن فاصلهي بين زمين و ماه يا ستارگان را اندازه بگيريم. بنابراين بايد به ساير امكاناتي توجه كنيم كه درعمل قابل استفاده است. اما در اينجا چه امكاناتي داريم؟ بهترين ابزار شناخته شده امواج الكترومغناطيسي است.
اگر مسير نور در فضا خط مستقيم باشد، در اينصورت به جرات ميتوانيم ادعا كنيم كه فضا اُقليدسي است. براي پي بردن به نوع انحناي فضا بايد مسير پرتو نوري را مورد بررسي قرار دهيم .
اما تجربه نشان ميدهد كه مسير نورهنگام عبوراز كنارماده يعني زماني كه از يك ميدان گرانشي عبورمیکند خط مستقيم نيست، بلكه منحني است. بنابراين فضاي اطراف اجسام اُقليدسي نيست. به عبارت ديگر ساختارهندسي فضا نااُقلیدسی است.
هندسه فراکتال
بَرخال یا فراکتال (Fractal) ساختاری هندسی است که با بزرگ کردن هر بخش از این ساختار به نسبت معین، همان ساختار نخستین به دست آید. به گفتاری دیگر برخال ساختاری است که هر بخش از آن ، با تمام آن همانند است. برخال از دور و نزدیک یکسان دیده میشود. به این ویژگی خودهمانندی گویند. برخالها یکی از ابزارهای مهم در گرافیک رایانهای هستند. واژه فراکتال مشتق گرفته شده از واژه لاتینی فراکتوس- به معنی سنگی که به شکل نامنظم شکسته شده باشد-.
در سال ۱۹۷۵ برای اولین بار توسط بنوآ مندلبرو مطرح شد. فراکتال ها شکلهایی هستند که بر خلاف شکلهای هندسی اُقلیدسی به هیچ وجه منظم نیستند. این شکلها اولاً سرتاسر نامنظماند، ثانیاً میزان بی نظمی آنها در همه مقیاسها یکسان است. با ملاحظه اشکال موجود در طبیعت، مشخص میشود که هندسه اُقلیدسی قادر به تبیین و تشریح اشکال پیچیده و ظاهراً بی نظم طبیعی نیست.
مندلبروا در سال ۱۹۷۵ اعلام کرده که ابرها به صورت کره نیستند، کوهها همانند مخروط نمیباشند، سواحل دریا دایره شکل نیستند، پوست درخت صاف نیست و صاعقه بصورت خط مستقیم حرکت نمیکند.

برخال از دید هندسی به چیزی گویند که دارای سه ویژگی زیر باشد:
- دارای ویژگی خودهمانندی باشد یا به انگلیسی self-similar باشد.
- در مقیاس خرد بسیار پیچیده باشد.
- بعد آن یک عدد صحیح نباشد. بعد خط یک، بعد صفحه دو و بعد فضا سه است. برخالها برخلاف همهی اینها بعد صحیح ندارند. برای نمونه بعد یک برخال میتواند ۱.۵ باشد به این دلیل از خط پیچیدهتر و از صفحه سادتر است. بعد برخال از یک سری فرمولهای لگاریتمی بدست میآیند.
سیستم ساختاری تکرار
این سیستم که دارای علامت اختصاری IFS – Iterated Function System – است، سیستم تکرار را مطرح میکند که به نوعی پایهی هندسه فرکتال است. تکرار یکی از راههای ایجاد فرم در معماری است اما در فرکتال این فرم بایستی دارای مشخصات هندسی که در قسمت هندسه فرکتال مطرح شد را دارا باشد.
بهطور کلی این تکرار میتواند از کنار هم قرار گرفتن یک شیء بدست آید یا اینکه یک موضوع نسبت به موضوع دیگر و بهطور متوالی کوچک شود.

خود متشابهی
شیئی را دارای خاصیت خود متشابهی میگوییم هر گاه قسمتهایی از آن با یک مقیاس معلوم، یک نمونه از کل شیئی باشد. سادهترین مثال برای یک شیئی خود متشابه در طبیعت گل کلم است که هر قطعهی کوچک گل کلم متشابه قطعه بزرگی از آن است.
همینطور درخت کاج یک شیئی خود متشابه است، چرا که هر یک از شاخههای آن درمقیاس بسیار کوچکترخیلی شبیه یک درخت کاج است. همچنین در مورد برگ سرخس نیز چنین خاصیتی وجود دارد. رشته کوهها، پشتههای ابر، مسیر رودخانهها و خطوط ساحلی نیز همگی مثالهایی از یک ساختمان خود متشابه هستند.
فراکتال شکل هندسی پیچیده است که دارای جزئیات مشابه در ساختار خود در مقیاسهای متفاوت میباشد و بی نظمی در آن از دور و نزدیک به یک اندازه است.
به طور مثال وقتی به یک کوه نگاه میکنیم شکلی شبیه به یک مخروط میبینیم که روی آن مخروطهای کوچکتر و بی نظمی دیده میشود ولی وقتی نزدیک میشویم همین مخروطهای کوچک شبیه کوه هستند یا شاخههای یک درخت شبیه خود درخت هستند.
البته در طبیعت نمونههای اجسام فراکتال فراوان است. و اگر به ساختههای دست بشر هم نگاه کنیم تراشههای سیلیکان یا مثلث سرپینسکی نیز فراکتال هستند؛ و در معماری همیشه نباید نیاز بشر را هندسهی اُقلیدسی تأمین کند. گسترش شهرها نمونه آشکاری از فراکتال است.
برخالها از نظر روش مطالعه به برخالهای جبری و بر خالهای احتمالاتی تقسیم میشوند. از طرف دیگر برخالها یا خود متشابه اند (self similarity) یا خود ناهمگرد (self affinity) هستند. در خود متشابهی، شکل جزء شباهت محسوسی به شکل کل دارد. این جزء، در همه جهات به نسبت ثابتی رشد میکند و کل را به وجود میآورد.
اما در خودناهمگردی شکل جزء در همه جهات به نسبت ثابتی رشد نمیکند. مثلاً در مورد رودخانهها و حوضههای آبریز بعد برخالی طولی متفاوت از بعد برخالی عرضی است.
از اینرو شکل حوضه آبریز کشیدهتر از زیر حوضههای درون حوضه است. به خودهمانندی همسانگرد (isotropy) میگویند. به خود ناهمگردی نا همسانگرد (anisotropy) میگویند.
کاربردها
از برخالها به منظور آسانسازی در کارهای وابسته به مدل سازی پیچیدگی در زمینههای گوناگون علمی و مهندسی استفاده میشود. اززمینههای مهم کاربردی گزینههای زیر را میتوان برشمرد:
- گرافیک رایانهای
- پردازش تصویر
- نظریهی موجکها
- تغییر شکل پلاستیک و شکست مواد
هندسهی ریمانی
هندسه ریمانی شاخهای از هندسه دیفرانسیل است که به بررسی خمینههای ریمانی میپردازد. یک خمینه ریمانی خمینهای است که مجهز به یک متریک ریمانی میباشد یعنی ضرب داخلی درفضای مماس برهرنقطه خمینه، به طور هموار تغییر میکند. هندسه ریمانی در قرن نوزدهم توسط برنهارد ریمان پایهگذاری شد.
هندسه ریمانی در نظریه نسبیت عام نقش پایهای دارد. هندسه ریمانی مهمترین و پرکاربردترین شاخهی هندسه دیفرانسیل میباشد. هندسهی ریمانی کاربردی یعنی هندسهای که در آن فضا و زمان خمیده است.
برای نمونه اگر خطی واقع بر سطح یک کره را در نظر بگیرید، از هیچ نقطه بیرون آن خط نمیتوان خطی به موازات خط نخست رسم کرد در حالی که درهندسه اُقلیدسی این کار کاملاً ممکن است. در این هندسه مجموع زوایای مثلث بیشتر از ۱۸۰ درجه است.

هندسه هُذلولوی
هندسه هذلولوی یکی از هندسههای نااُقلیدسی است که به هندسه لباچفسکی نیز مشهور است. نام انگلیسی این نوع هندسه، یعنی (Hyperbolic)، از کلمه یونانی هیپربالئین به معنی “افزایش یافتن” گرفته شدهاست که در آن فاصلهی میان نیمخطها دراصل توازی افزایش مییابد.
هدف از ابداع هندسه هذلولوی پیدا کردن مدل هندسی بود که در آن برای هر نقطه و هر خط تعداد نامتناهی خط گذرنده ازنقطه وعمود به خط موجود باشد. در بعد دو مدلهای اساسی هندسه هذلولوی عبارتند از دیسک پوانکاره و نیم صفحه بالا. سازگاری هندسه هذلولوی، استقلال منطقی اصل توازی را از سایر اصول هندسه اُقلیدسی نشان میدهد.

نیم صفحهی بالا
در این مدل هندسه هذلولوی، کوتاهترین مسیرها (ژئودزیکها) عبارتند از خطهای عمودی و نیم دایرههای عمود بر محورx. در هندسه ریمانی چنین هندسهای با متریک ریمانی زیر به دست میآید.

انحنای این متریک ثابت و برابر 1- میباشد .
هندسه جبری
هندسهی جبری شاخهای ازریاضیات است که مفاهیم جبر مجرد، بهویژه جبر جابجایی، را با مسائل هندسه میآمیزد. این شاخه از ریاضیات جدید با آنالیز مختلط، توپولوژی و نظریه اعداد در ارتباط تنگاتنگ است
. واریتهی مستوی (آفین) n-بعدی که یکی از بنیادیترین مفاهیم این شاخه از ریاضی است، دقیقاً صفرهای مشترک تعدادی دلخواه از چندجملهایهای n-متغیره روی میدان مفروض تعریف میشود؛ بنابراین، حلقهی چندجملهایها نقش عمدهای در هندسهی جبری ایفا میکند.
تاریخ این علم گسترش فراوانی دارد، بهطوریکه قسمتی از مطالعات ارشمیدس مسائلی پیرامون مقاطع مخروطی را تشکیل میداد. همچنین، ابن هیثم، فیزیکدان مسلمان عرب سدهٔ ۱۰ میلادی، برای محاسبهی مسافتها مجبور به استفاده از معادلات درجهی سوم میشده است؛ و نهایت اینکه خیام معادلهی درجهی سوم را در کلیترین حالت حل کرد. او این کار را از طریق مقاطع مخروطی، و قطع دادنِ دایره با سهمیِ درجهی دوم انجام داد.
هندسه دیفرانسیل
هندسهی دیفرانسیل زمینهای ازریاضیات است که به بررسی ویژگیهای خمینهها میپردازد. خمینهها که مفهوم تعمیمیافته از رویهها در ابعاد بالاتر هستند، مهمترین مفهوم مورد بحث هندسه دیفرانسیل میباشند.
هندسه تحلیلی
هندسه تحلیلی شاخهای از ریاضیات است که از ترکیب هندسه وجبر مقدماتی به وجود آمده است. در این رشته اشکال هندسی و روابط بین آنها را با مقادیر و معادلات عددی و جبری بیان میکنند. بنیانگذاران این مبحث، دکارت و فرما در قرن ۱۷ میلادی بودهاند. در هندسهی تحلیلی ابتدا با تعریف صفحهی یک بعدی و دو بعدی آشنا می شویم و نقاط را به وسیلهی مختصات عددی نمایش میدهیم. این رشته در مورد اندازه، فاصله و زاویه، فرمولهای مربوط به خود را دارد.
هندسه محاسباتی یکی از شاخههای علوم کامپیوتر است. هندسه محاسباتی علم حل مسائل هندسی به روش الگوریتمی و با استفاده از ساختمان دادهها (Data Structures) میباشد. بعضی از مسائل کاملاً هندسی، برآمده از مطالعهٔ الگوریتمهای هندسهٔ محاسباتی است و مطالعه اینگونه مسائل نیز به عنوان بخشی از هندسه محاسباتی به حساب میآید.
هندسه محاسباتی
انگیزهی اصلی برای قلمداد کردن هندسه محاسباتی به عنوان یک رشتهی علمی، پیشرفت در گرافیک کامپیوتری، طراحی و تولیدات با کمک رایانه (به وسیلهی نرمافزارهایی مانند کد/کم) بود؛ ولی طبیعتاً بسیاری از مسائل در هندسه محاسباتی، قدیمی هستند.
کاربردهای مهم دیگر هندسه محاسباتی در دانش روباتیک (برنامهریزی حرکتی)، سیستمهای اطلاعات جغرافیایی(جستجو و مکانیابی هندسی، نقشهکشی راهها)، طراحی مدار مجتمع(طراحی و بازبینی هندسی مدارهای مجتمع) و مهندسی با کمک رایانه (برنامهریزی ماشینهای کنترل عددی) میباشد.
شاخههای اصلی هندسه محاسباتی
- هندسهی محاسباتی ترکیبی (هندسه الگوریتمی): این هندسهی محاسباتی اشیای هندسی را به عنوان موجودات گسسته در نظر میگیرد. براساس کتابی که توسط پرپاراتا و شاموس نوشته شدهاست، لفظ هندسه محاسباتی با این مفهوم، نخستین بار در سال ۱۹۷۵ بیان شدهاست.
- هندسه محاسباتی عددی (هندسه ماشینی، طراحی هندسی با کمک رایانه یا مدلسازی هندسی): اساس کار این هندسه محاسباتی به این صورت است که اشیای دنیای واقعی را به صورت مناسبی برای محاسبات رایانهای در سیستمهای کد/کم در میآورد. این شاخه ممکن است به عنوان هندسه توصیفی پیشرفته در نظر گرفته شود و اغلب یکی از شاخههای گرافیک کامپیوتری یا کَد به حساب میآید. هندسه محاسباتی با این معنا، از سال ۱۹۷۱ مورد استفاده قرار گرفت.




10 Comments
سلام
کاربرد هندسه تحلیلی را به صورت کامل بیان میکنید ممنون میشم با تشکر
سلام بر شما کاربر گرامی
شاخه هندسه ی تحلیلی در واقع ترکیبی از جبر و هندسه میباشد.
در این شاخه از هندسه به مفاهیم مختصات، بردارها در صفحه و فضا، معادلات خط و حرکت پرتابه ها در فضا و… میپردازد. با کمی دقت به مباحث ذکر شده و زیر شاخه های آن در هندسه تحلیلی، میتوان به کاربرد این شاخه از ریاضیات در رشته هایی اعم از هوافضا، فیزیک و… اشاره کرد.
موفق و موید باشید.
سلام روزتون بخیر باشه منابعی که برای جمع آوری مطالب بالا استفاده کردین رو میتونین در اختیار من هم قرار بدین؟
سلام بر شما کاربر محترم
کتاب هندسه های اُقلیدسی و برخی مقالات و سایت های معتبر علمی. فیزیکِ کتاب رو دارم اما pdf اون رو ندارم که براتون به اشتراک بذارم مقالات معتبر هم سعی کنید در سایتهای علمی از جمله library genesis جستجو کنید.
آرزوی موفقیت برای شما
سلام وقت بخیر ببخشید میشه در مورد تاریخچه علم هندسه وکاربردش مقاله وکتاب بهم معرفی کنید ؟
خیلی هم عالی.
هندسه خطی چیه؟
سلام خانم فرزامی.
مقاله یا کتابی راجب هندسه جبری و تاریخچش میتونید معرفی میکنید؟
سلام هستی خانم
1- کتاب های الکساندر گروتندیک(Alexander Grothendieck).
2- هندسه جبری(Algebraic Geometry)، نویسنده: Daniel Bump
3- Reid M. Undergraduate algebraic geometry
بسیار عالی متشکرم
خواهش میکنم.