نوار موبیوس چیست؟ + کاربرد آن

در این مقاله قصد داریم تا به کاربرد نوار موبیوس در معماری و تعریف آن بپردازیم.آگوست فردیناند موبیوس (August Ferdinand Möbius) در روز ۱۷ نوامبر ۱۷۹٠ در شهر زاکسن به دنیا آمد. وی ریاضیدان و ستاره شناس مشهور آلمانی است. بیشتر شهرت او به دلیل کشف نوار موبیوس است.

آگوست فردیناند موبیوس
August Ferdinand Möbius
نوار موبیوس (mobius strip ) چیست؟
نوار موبیوس نواری است که دو لبه آن بر هم قرار گرفته و حلقهای را به وجود میآورد؛ البته باید یک لبه انتهایی قبل از اتصال به لبه دیگر نیم دور چرخانده شود. این نوار را دو ریاضیدان آلمانی به نامهای آگوست فردیناند موبیوس و جان بندیکت (Johann Benedict) در سال ۱۸۵۸ به طور مستقل و جداگانه کشف کردند و به ثبت رساندند.
روش ساخت نوار موبیوس
ابتداییترین راه برای ایجاد این نوار، انتخاب یک نوار مستطیل شکل و نرمی است که آن را یک بار میپیچانیم و سپس دو انتهای آن را به هم متصل میکنیم. سطحی که به این ترتیب به دست میآید «نوار موبیوس» نامیده میشود.

این سطح تنها یک رو دارد. به بیان دیگر، یک صفحه کاغذی را میتوان با دو رنگ گوناگون در دو طرف آن رنگ کرد اما نوار موبیوس را با این روش نمیتوان با دو رنگ مختلف رنگ کرد. در صورت اقدام به چنین کاری به همان جایی که رنگ کردن را در ابتدا آغاز کرده بودیم، میرسیم؛ در حالی که در طرف دیگر نوار هستیم! پس نوار موبیوس، سطحی است که یک رو دارد و حرکت ما روی آن تا بینهایت بار تکرار می شود.
تعریف ریاضی نوار موبیوس – mobius strip
دلیل «یک رویه بودن» این نوار آن است که در هر نقطه a از نوار موبیوس میتوان دو بردار با جهتهای مختلف رسم کرد که بر نوار موبیوس در این نقطه عمود باشد. این بردارها را قائمهای نوار موبیوس در نقطه a مینامیم.
یکی از این بردارها را انتخاب و نقطه a را به تدریج روی نوار موبیوس جابجا میکنیم. در این صورت بردار ما هم همراه با نقطه a جابجا میشود. بنابراین، روی نوار موبیوس چنان مسیر بستهای وجود دارد که اگر قائمی این مسیر را روی سطح بپیماید، به جای این که به وضع نخستین خود برسد، روی برداری که در جهت مخالف وضع نخستین آن است قرار میگیرد.
مرز یک ناحیه در فضا
مرزِ یک ناحیه، خط جدا کننده آن ناحیه از ناحیه دیگر است. در ریاضیات برای یک سطح سه مفهوم تعریف می شود:
۱- نقطه داخلی: نقطه ای که بتوان آن را داخل یک دایره روی سطح محصور کرد.
۲- نقطه خارجی: نقطه ای است که بتوانیم دایره ای حول آن رسم کنیم که متعلق به آن سطح نباشد.
۳- نقطه مرزی: نقطه ای است که هر دایره ای حول آن رسم شود، قسمتی از آن متعلق به سطح و قسمت دیگر آن متعلق به خارج آن سطح باشد.
با این تعریف نوار موبیوس فقط یک مرز دارد. یعنی با یک بار حرکت در کرانههای انتهای نوار تمام مرز آن را می توانیم طی کنیم.
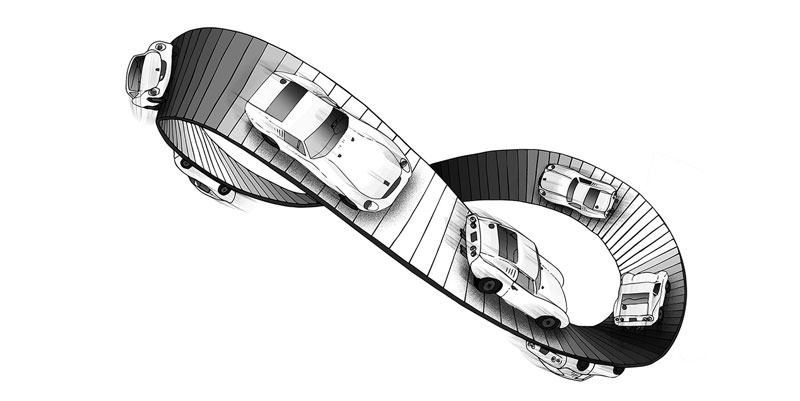
نکاتی در رابطه با نوار موبیوس – mobius strip
اگر با یک خودکار بر روی نوار موبیوس خطی در طول نوار بکشیم و ادامه دهیم این خط دوباره به نقطه شروع باز میگردد و هر دو طرف نوار خط کشیده میشود! در واقع، نوار موبیوس مثالی از یک رویه بدون جهت (جهت ناپذیر) است. یعنی نوار موبیوس سطحی است که یک رو دارد.
نوار موبیوس خواص غیرمنتظره دیگری نیز دارد؛ برای نمونه، هرگاه بخواهیم این نوار را در امتداد طولش بِـبُریم به جای این که دو نوار به دست بیاوریم، یک نوار بلندتر و با دو چرخش به دست می آوریم! همچنین با تکرار دوباره این کار دو نوار موبیوس در هم پیچ خورده به دست میآید. با ادامه این کار یعنی بریدن پیاپی نوار، در انتهای کار تصاویر غیرمنتظرهای ایجاد میشود که به حلقههای پارادرومیک (paradromic rings) موسومند. همچنین اگر این نوار را از یک سوم عرض نوار ببریم، دو نوارِ موبیوس در هم گره شده با طولهای متفاوت به دست خواهیم آورد. تمامی این کارها به آسانی قابل اجراء هستند.
نوار موبیوس را میتوان حالت خاصی از بطری کلاین دانست.نوار موبیوس به نوعی میتواند به عنوان سمبل تعامل دوگانگی فرهنگی تلقی شود.
کاربرد نوار موبیوس در معماری
خاصیت موبیوسی: خاصیتی است که رابطه بین «درون» و «بیرون» را وارونه میکند. یعنی هر نقطه از یک سطح موبیوسی در عین حال که درون است، بیرون نیز میباشد! بنابراین در یک تغییر پیوسته، نوعی دگرگونی در ماهیت یک فضا صورت میگیرد.
در واقع در این حالت فضا خاصیت دو گانه اما پیوسته پیدا میکند. خاصیت موبیوس که گذر از درون به برون و از برون به درون را ممکن میکند، کمابیش توانسته است بر فراز شکاف حاصل از دوگانگی (ثنویت) پلی بزند (شایگان،۱۳۸٠). بنابراین، فضای ِمیان «برون و درون»، «پیوستگی» و «تکرار» با یک تعریف ریاضی به یک سطح هندسی تبدیل میشود. سطحی که بر آن در هر لحظه ای هم داخل و هم خارج فضا هستیم. این ویژگی در طراحی معماری مورد توجه قرار گرفته است




10 Comments
سلام میخواستم بپرسم آیا از نوار موبیوس در طیف های فرکانسی در بازه زمان کاربرد دارد آیا به انالیز ارتعاشات در وضعیت فرکانسی کاربرد دارد؟
متشکر
پس شاید بشه موضوع سفر در زمان رو با نوار موبیوس نمونه سازی کرد. شاید…
آره اگه بشه بازگشت به نقطه ابتدا و طیف حرکت ارتعاشات و فرکانس ها رو در نظر گرفت و…
در کل یعنی آره شاید بشه برای سفر در زمان نوار موبیوس رو هم در کنار دیگر مباحث در نظر گرفت
هیجان انگیزه مگه نه؟
من عااااااااااااااااااااشق ریاضی بودم و هستم اما سرنوشت منو یک معمار کرد. اینکه معماری رو هم دوست داشتم دلیل شد الان اینجا باشم اما من خیلی دلم ذیاضیات محض یا کاربردی رو میخواست که به دلایلی نشد این رشته رو بخونم..
انقدرررر عاشق ریاضی هندسه و همه زیرمجموعه هاش بودم و هستم که خدا میدونه. هی نوار موبیوس رو میساختم و مداد میکشیدم و یا سه ردیف خط میکشیدم و قیچی ش میکردم و وقتی دوتا نوار میدیدم ذوق میکردم و هی اینکار رو تکرار میکردم! از خدا میخوام کمکم کنه انشالله ارشد رو بتونم معماری تکنولوژی قبول بشم شدیدا علاقه دارم روی موبیوس مطالعه کنم و بعنوان تحقیق مقاله و یا اگه بشه پروژه از این موضوع بهره ببرم.
میخوام فاصله بین منو ریاضی از بین بره. بازم میگم دلم برا دنیای ریاضیات خیییییییییییییلی تنگ شده تو این مدت دانشجویی مخصوصا رشته ی من مهلت نداشتم برگردم و یکم ریاضیات بخونم..!
درود بر شما
اینکه به ریاضی علاقه مندید باعث خرسندیست
از طرفی، معماری هم بی فاصله از ریاضیات نیست و هنر هندسه در ریاضیات به خوبی در آن قابل رویت است.
برای شما آرزوی موفقیت در هر عرصه ای که به آن علاقه مند و توانمندین را دارم.
آیا رابطه ای هست که بتونه این پدیده رو از نظر محاسباتی یا هندسی نشون بده تا بتونیم تو بعضی از کارها ازش استفاده کنیم؟
مثل: https://en.wikipedia.org/wiki/M%C3%B6bius_strip
ولی منظم تر . . .
با تشکر فراوان، ممنون . . .
سلام مخاطب گرامی
رایطه های پارامتری و قطبی سیلندری که در ویکی پدیا امده است نوار موبیوس را به بهترین نحو توصیف می کنند. البته نوار موبیوس به صورت توپولوژیکی هم توصیف می شود که تخصصی تر است. به عنوان مثال، نوار موبیوس مثال خوبی از یک منیفلد فشرده مرزدار جهت ناپذیر است.
چه موضوع جالبی.
کاش ریاضی فرمول نداشت خیلی دیر تو مغزم میره
متشکرم
ریاضی بدون فرمول !!!!
ریاضی علمی بینهایت زیباست و بسیار کاربردی
از اینکه خیلی کامل توضیح دادید ممنون.عکس های خوبی هم گذاشتید