بررسی تاریخچه نماد انتگرال

همهی ما دستکم در دوران دبیرستان (متوسطه دوم) با مفهوم انتگرال آشنا شدهایم. انتگرال نیز همچون مفاهیم دیگر ریاضی به دلیل اهمیتی که دارد شایسته داشتن یک نماد بوده است. چنانکه میدانید نماد انتگرال به این شکل (∫) است. اما شاید ندانید که این نماد از چه زمانی رایج شده و چه سرگذشتی داشته است. در این نوشته با ما همراه باشید تا تاریخچه انتگرال و نماد معروف آن را با هم مرور کنیم.
تاریخچهی انتگرال
پیش از آن که تاریخچه نماد انتگرال را بررسی کنیم، ابتدا سابقه مفهوم انتگرال را بررسی میکنیم. هنگامی که تاریخ ریاضیات را ورق میزنیم، نخستین اشارهای که به مفهوم انتگرال مشاهده میکنیم، مربوط به دست خطی به نگارش لایبنیتز است.
گوتفرید ویلهلم لایبنیتز (Gottfried Wilhelm Leibniz) (۱۶۴۶–۱۷۱۶)، فیلسوف، ریاضیدان و فیزیکدان آلمانی بود که همچنین نقش بهسزایی در سیاست اروپایی زمان خویش بازی کرده است و مقام بالایی نیز در تاریخ فلسفه و تاریخ ریاضی دارد. این ریاضیدان مشهور قرن هفده میلادی مشهور به لایبنیتز، نام خود را از شهر محل تولد خود گرفته است. شهر لایبنیتز اینک در جنوب اتریش در ایالت اِستیریا قرار دارد.
لایبنیتز در نوشتهای که در تاریخ 29 اکتبر 1675 (برابر با سهشنبه 7 آبان ماه سال 1054 هجری شمسی) نوشته، نماد انتگرال را ابداع نموده است. نسخهای خطی از این نوشته موجود است که البته با توجه به گذر زمان و آثار آب خوردگی، خواندن آن دشوار است:

لایبنیتز در این نامه نماد انتگرال (∫) را به همراه چند مفهوم دیگر جهت یادآوری برای خود نوشته است. وی در طی سالهای 1672 تا 1676 در پاریس مقیم بوده است و این دستخط نیز در همین زمان از وی بر جا مانده است. این دستخط سالها بعد در شهر هانوفر آلمان کشف شده و توسط کارل ایمانوئل گرهارت در نیمههای قرن نوزدهم میلادی چنین نسخهبرداریشده است:

لایبنیتز دراین نوشته انتگرالی را معرفی کرده است که هماکنون همه ما این انتگرال را میشناسیم:
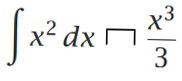
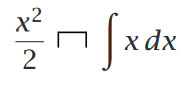
نماد انتگرال (∫) در همه کشورها به صورت واحدی نوشته نمیشود. در زبان انگلیسی این نماد تا حدودی به سمت راست متمایل است. در حالیکه در زبان آلمانی قائم است و در روسیه نیز متمایل به سمت چپ نوشته میشود.
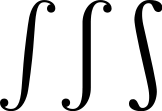
این نماد، به گونههای مختلفی به کار می رود که درزیرآورده ایم:
| نماد | توضیح |
|---|---|
| \(\int \int \) | انتگرال دوگانه |
| \(\int \int \int\) | انتگرال سه گانه |
| \( \int \int \int \int \) | انتگرال چهارگانه |
| \(\oint \) | انتگرال کانتور(روی مسیر) |
| انتگرال سطحی | |
| انتگرال حجمی | |
| انتگرال ساعت گرد | |
| انتگرال پاد ساعت گرد | |
| انتگرال کانتور ساعت گرد | |
| انتگرال کانتور پاد ساعت گرد |
انتگرال نيز مانند مشتق داراي قواعد و حالتهاي خاص است كه بايستي آنها را فرا بگيريد. اگر بخواهيم همزمان دو عمل مشتق گيري و انتگرال گيري را روي تابعي انجام دهيم، در واقع هيچ كاري انجام نداده ايم زيرا اين دو عمل يكديگر را خنثي ميكنند.




6 Comments
انتگرال سطحی و حجمی به بعد علامت ندارن؟
سلام
عالی بود ممنون
بسیار عالی و تشکر ویژه از سرکار خانم فرزامی و وب سایت وزینشان
افسوس که دانش اموزان قدر علوم پایه را نمیدانند و سعی تلاششان معطوف به رشته های مهندسی و پزشکی است.
اما غافلند که خوارک علمی یک مهندس و یا یک پزشک را متخصصان علوم پایه نظیر ریاضیات محض فیزیک محض شیمی محض تامین میکنند
بسیار متشکرم از حُسن نظر شما. بله همینطوره ریاضی سرشار از زیباییست و پایه ای برای سایر علوم مهندسی. امیدوارم در مسیر پیش رو بتوانم قدمی بردارم.
جالب بود.سایت خیلی خوبی دارید.من که خوشم اومد
متشکرم.